PyTorch深度学习实践Part3——梯度下降算法

优化问题

  1. 上讲是穷举所有可能值并肉眼搜索损失最低点。

  2. 分治法可能错失关键，最终只找到局部最优

    穷举和分治都不能有效解决大数据

  3. 梯度(gradient)决定权重w往哪个方向走，梯度即成本对权重求导，为了控制步伐需要设定一个较小的学习率。

    image-20210116203946162

  4. 在大量的实验中发现，其实很多情况下，我们很难陷入到局部最优点。但是存在另外一个问题，鞍点。鞍点会导致无法继续迭代，可以选择通过引入动量解决。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 1.0


def forward(x):
    return x * w


def cost(xs, ys):
    cost = 0
    for x, y in zip(xs, ys):  # 3行数据
        y_pred = forward(x)
        cost += (y_pred - y) ** 2  # 累加损失平方
    return cost / len(xs)  # 平均


def gradient(xs, ys):
    grad = 0
    for x, y in zip(xs, ys):
        grad += 2 * x * (x * w - y)  # 成本对权重求导
    return grad / len(xs)


print('Predict(before training)', 4, forward(4))
mse_list = []  # 保存损失的变化曲线
for epoch in range(100):
    cost_val = cost(x_data, y_data)  # 计算损失
    mse_list.append(cost_val)  # 记录损失变化
    grad_val = gradient(x_data, y_data)  # 计算梯度
    w -= 0.01 * grad_val  # 改善权重
    print('Epoch:', epoch, 'w=', w, 'loss=', cost_val)
print('Predict(after training)', 4, forward(4))

# 图表打印
plt.plot(range(100), mse_list)
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.show()

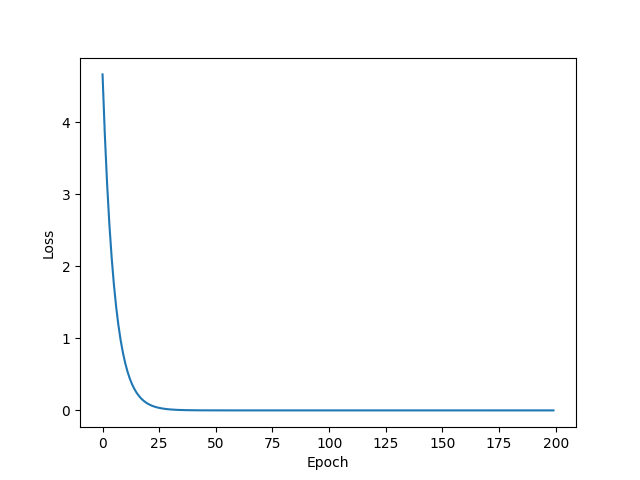
image-20210116215632394

  1. 绘图时想要消除局部震荡，可以使用指数加权均值方法，使其变成更加平滑的曲线
  2. 如果训练的图像发散，则表明这次训练失败了。其原因有很多，比如，学习率取太大。

随机梯度下降

使用梯度下降方法时，更加常用随机梯度下降(Stochastic Gradient Descent)。

随机梯度下降也是跨越鞍点的一种方法，同时也可以大幅减少计算量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import matplotlib.pyplot as plt
import random

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 1.0


def forward(x):
    return x * w


def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2


def gradient(x, y):
    return 2 * x * (x * w - y)


print('Predict(before training)', 4, forward(4))
mse_list = []  # 保存损失的变化曲线
for epoch in range(100):
    x, y, i = 0, 0, random.randint(0, 2)
    # 样本原本就是随机的，所以不需要打乱样本
    for m, n, j in zip(x_data, y_data, range(0, 2, 1)):
        if j == i:
            x, y = m, n  # 3组中随机选取一组
            break
    grad = gradient(x, y)  # 计算梯度
    w -= 0.01 * grad  # 改善权重
    cost_val = loss(x, y)  # 计算损失
    mse_list.append(cost_val)  # 记录损失变化
    print('Epoch:', epoch, 'w=', w, 'loss=', cost_val)
print('Predict(after training)', 4, forward(4))

# 图表打印
plt.plot(range(100), mse_list)
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.show()

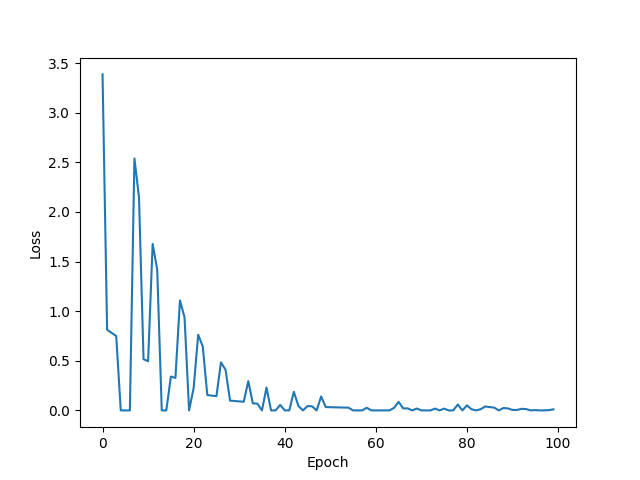
image-20210116222847776

随机梯度下降可能享受不到并行计算的效率加成，因此会使用折中方法，批量随机梯度下降(Mini-Batch/Batch)