OpenCV-Part3
OpenCV-Part3——图像处理(中)
[TOC]
图像边缘检测
边缘检测
- 边缘是图像中的重要的结构性特征,边缘往往存在于目标和背景之间、不同的区域之间,因此它可以作为图像分割的重要依据。
- 边缘检测是检测图像中的像素点,其周围的像素值是否发生了急剧的变化,这个剧烈的变化就是不同物体的边界。
- 边缘其实就是图像上灰度级变化很快、梯度很大的点的集合。
- 图像的梯度可以用一阶导数和二阶偏导数来求解。
- 边缘检测提取的是图像中不连续部分的特征,将闭合的边缘提取出来便可以作为一个区域。
- 与区域划分相比,边缘检测不需要逐个的对像素进行比较,比较适合大图像的处理。
- 图像数据以二/三维矩阵的形式存储的,对一幅图像的求导相当于对一个曲面求导。
- 对图像求导、获取一幅图像的梯度:使用模板(Roberts、Prewitt、Sobel、Lapacian算子)对原图像进行卷积。
- OpenCV 提供的梯度滤波器(高通滤波器):Sobel、Scharr、Laplacian、Canny。
- 使用一阶导的算子有 Prewitt、Sobel、Canny;使用二阶导的有 Lapacian 。Scharr 是对 Sobel(使用小的卷积核求解求解梯度角度时)的优化。
各种算子比较
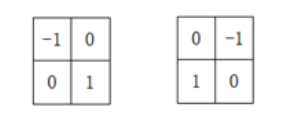
Roberts 算子
- Roberts 算子又称为交叉微分算子,是基于交叉差分的一阶微分算子。比较简单,计算量小。
- Roberts 常用来处理具有陡峭的低噪声图像,当图像边缘接近于正 45° 或负 45° 时,该算法处理效果更理想。其缺点是对边缘的定位不太准确,提取的边缘线条较粗。
- 对应的模板:
Prewitt 算子
Prewitt 算子也是一种一阶微分算子。由 Roberts 的 2×2 改为 3×3 模板矩阵,增加了计算量。
Prewitt 在水平方向和垂直方向分别利用两个方向模板与图像进行邻域卷积,边缘检测效果比 Robert 算子更加明显。
Prewitt 在权重上对局部像素进行了平均,对噪声有抑制作用。但是同时像素平均也代表了对图像的低通滤波,所以 Prewitt 算子对边缘的定位不如 Roberts 算子。
Prewitt 会造成边缘点的误判,因为许多噪声点的灰度值也很大。而且对于幅值较小的边缘点,其边缘反而丢失了。
对应的模板:
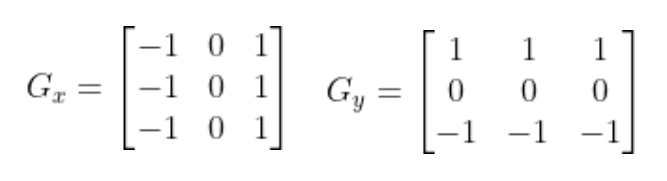
Sobel 算子
Sobel 是结合了高斯平滑与微分求导的一阶微分算子。在 Prewitt 基础上,将权值改为符合高斯分布。
Sobel 考虑了不同距离的相邻点对当前像素点的影响,距离越近的像素点对应当前像素的影响越大,从而实现锐化边缘。因此,比 Prewitt 和 Roberts 都更能准确检测图像边缘。
Sobel 算子根据像素点上下左右邻点灰度加权差,在边缘处达到极值这一现象检测边缘,对噪声具有平滑作用,并提供较为精确的边缘方向信息。
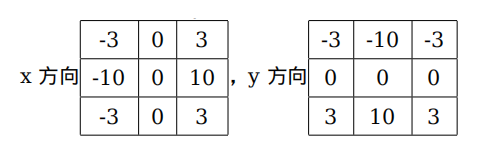
对应的模板:
1 | img = cv2.imread('box.png', 0) |
Laplacian 算子
拉普拉斯(Laplacian)是一个二阶微分算子,是二阶 Sobel 导数,常用于图像增强和边缘提取。
Laplacian 原理:在卷积邻域内,如果中心像素的灰度更高,则提升中心像素的灰度;反之则降低中心像素的灰度。
- 模板与图像进行卷积运算:当中心像素灰度等于邻域内其他像素的平均灰度时,结果为0;当中心像素高于平均灰度时,结果为正数;当中心像素低于平均灰度时,结果为负数。
- 对上述卷积运算结果用适当的衰弱因子处理后,加在原中心像素上,就可以实现图像的锐化处理。
Laplacian 算子模板分为四邻域和八邻域,四邻域是对邻域中心像素的四方向求梯度,八邻域是对八方向求梯度。
- 四邻域模板:
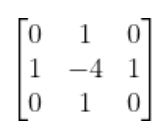
- 八邻域模板:
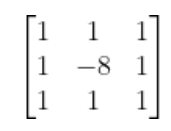
- 四邻域模板:
Laplacian 用于图像增强时,有这几个比较适合的场合。
- 由于是通过二次微分正峰和负峰之间的过零点来确定边缘线的位置,因此对孤立点或端点更为敏感,这一特性适用于以突出图像中的孤立点、孤立线或线端点为目的的场合。
- 用来改善因扩散效应的模糊特别有效,因为它符合降制模型。扩散效应是成像过程中经常发生的现象。
Laplacian 用于边缘提取时,一般不使用其原始形式。它对于边缘和噪声都非常敏感,在锐化边缘的同时也会增强图像中的噪声,所以需要先对图像进行平滑处理。
- 原因:1. Laplacian 对噪声具有无法接受的敏感性;2. 同时其幅值产生算边缘,这是复杂的分割不希望有的结果;3. 不能检测边缘的方向。
- 取而代之,一般使用的是高斯型拉普拉斯算子(Laplacian of a Gaussian,LoG),利用该LoG算子进行卷积 等价于 高斯模糊+拉普拉斯。所以,在 LoG 中使用高斯函数的目的就是对图像进行平滑处理,使用 Laplacian 的目的是提供一幅由零交叉确定边缘位置的图像。图像的平滑处理减少了噪声的影响,并且还抵消由 Laplacian 算子的二阶导数引起的逐渐增加的噪声影响。
Laplacian 用于图像分割时的作用:
- 利用它的零交叉性质进行边缘定位。
- 确定一个像素是在一条边缘暗的一面还是亮的一面。
图像锐化处理的作用是使灰度反差增强,从而使模糊图像变得更加清晰。图像模糊的实质就是图像受到平均运算或积分运算,因此可以对图像进行逆运算,如微分运算能够突出图像细节,使图像变得更为清晰。
由于拉普拉斯是一种微分算子,它的应用可增强图像中灰度突变的区域,减弱灰度的缓慢变化区域。因此,锐化处理可选择拉普拉斯算子对原图像进行处理,产生描述灰度突变的图像,再将拉普拉斯图像与原始图像叠加。最终结果是使图像中的各灰度值得到保留、灰度突变处的对比度得到增强,在保留图像背景的前提下,突现出图像中小的细节信息锐化图像。
1 | img = cv2.imread('box.png', 0) |

注意事项
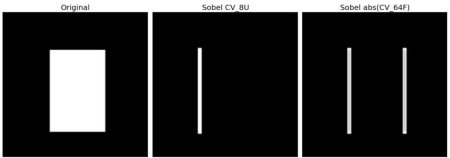
对于使用数据类型为
cv2.CV_8U或np.uint8,会有一个小问题:黑色到白色的过渡被视为正斜率(具有正值),而白色到黑色的过渡被视为负斜率(具有负值)。因此,当将数据转换为np.uint8时,所有负斜率均设为零,即错过这一边缘信息。如果要检测两个边缘,更好的选择是将输出数据类型保留为更高的形式,例如
cv2.CV_16S,cv2.CV_64F等,取其绝对值,然后转换回cv2.CV_8U。
1 | img = cv2.imread('box.png', 0) |
Canny边缘检测算子
基本原理
Canny 算子是一个具有滤波、增强、检测的多阶段的边缘检测算子。其产生的边缘很细,没有强弱之分,边缘检测性能比前面几种都要好。
Canny 的具体算法步骤:
用高斯滤波器平滑图像;
- 去除噪声。由于边缘检测很容易受到噪声影响,所以第一步是使用 5x5 的高斯滤波器去除噪声。
用一阶偏导的有限差分来计算并记录梯度和幅值方向;
对平滑后的图像使用 Sobel 算子计算水平方向和竖直方向的一阶导数(图像梯度)Gx 和 Gy 。根据得到的这两幅梯度图 Gx 和 Gy 找到边界的梯度和方向,公式如下:
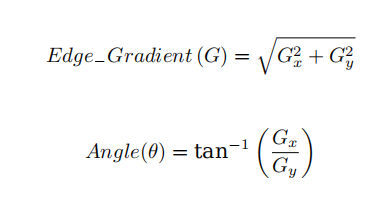
梯度的方向一般总是与边界垂直。梯度方向被归为四类:垂直,水平,和两个对角线。
对梯度幅值进行非极大值抑制:
在获得梯度的方向和大小之后,应该对整幅图像做一个扫描,去除那些非边界上的点。对每一个像素进行检查,看这个点的梯度是不是周围具有相同梯度方向的点中最大的。
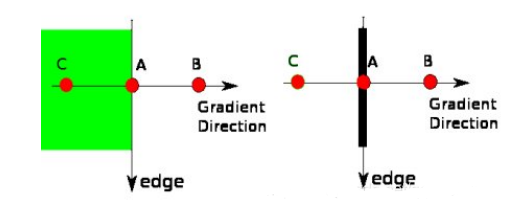
现在你得到的是一个包含“窄边界”的二值图像。
用双阈值算法检测和连接边缘:
现在要确定那些边界才是真正的边界。这时我们需要设置两个阈值:minVal 和 maxVal。当图像的灰度梯度高于 maxVal 时被认为是真的边界,那些低于 minVal 的边界会被抛弃。如果介于两者之间的话,就要看这个点是否与某个被确定为真正的边界点相连,如果是就认为它也是边界点,如果不是就抛弃。
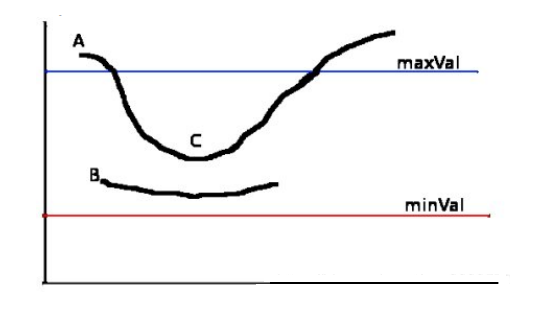
A 高于阈值 maxVal 所以是真正的边界点,C 虽然低于 maxVal 但高于minVal 并且与 A 相连,所以也被认为是真正的边界点。而 B 就会被抛弃,因为他不仅低于 maxVal 而且不与真正的边界点相连。所以选择合适的 maxVal和 minVal 对于能否得到好的结果非常重要。在这一步一些小的噪声点也会被除去,因为我们假设边界都是一些长的线段。
OpenCV中的Canny检测
cv2.Canny(src, threshold1, threshold2):封装了 Canny 的所有步骤。threshold1, threshold2:即双阈值算法的 minVal 和 maxVal 。perture_size:用于查找图像渐变的 Sobel 内核的大小。默认为3。L2gradient:用于查找梯度幅度的方程式。如果为True,则使用更精确的公式,默认为False。
1 | edges = cv2.Canny(img, threshold1=100, threshold2=200) # 建议放入彩色图 |
图像金字塔
定义
- 图像金字塔,是同一图像、不同分辨率的图像的集合。
- 图像金字塔,可以协助同时在不同分辨率的相同图像中进行目标检测,即同时检测不同大小的对象,因为我们不能确定对象将会以多大的尺寸显示在图像中。
构造图像金字塔
构造图像金字塔一般包括二个步骤:
- 利用低通滤波器平滑图像
- 对平滑后的图像进行采样
有两种采样方式:上采样(分辨率逐级升高,不会恢复细节信息)和下采样(分辨率逐级降低,会丢失细节信息)。
使用函数
cv2.pyrDown()和cv2.pyrUp()构建图像金字塔。cv2.pyrDown():从一个高分辨率大尺寸的图像向上构建一个金子塔(尺寸变小,分辨率降低)。cv2.pyrUp():从一个低分辨率小尺寸的图像向下构建一个金子塔(尺寸变大,但分辨率不会增加)。
下采样过后的层也称为 Octave 。
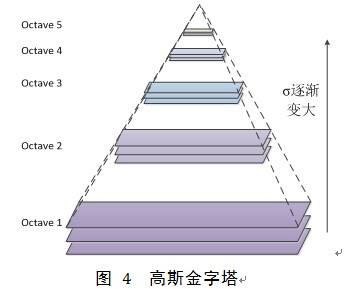
高斯金字塔
- 高斯金字塔的构造过程:
- 用高斯内核与图像卷积。
- 删除所有偶数行列。
- 此时
higher_reso与higher_reso2是不一样的,因为一旦进行下采样就丢失了细节信息。
1 | higher_reso = cv2.imread('messi5.jpg') |
拉普拉斯金字塔
- 拉普拉斯金字塔由高斯金字塔的高低层级差形成,仅为图像边缘信息。
- 拉普拉斯金字塔可以用于图像压缩。
使用金字塔进行图像融合
- 金字塔另一种常用的应用是图像融合。将两个不同层级或不同图像的 Octave 经过变换成相同大小并堆叠在一起,这可以使图像获得不同的特征数据(特征融合)。
- 加载两个图像
- 查找两个图像的高斯金字塔(在此示例中, 级别数为6)
- 在高斯金字塔中,找到其拉普拉斯金字塔
- 然后在每个拉普拉斯金字塔级别中加入A的左半部分和B的右半部分
- 最后从此联合图像金字塔中重建原始图像。
1 | import cv2 |
图像轮廓
轮廓定义
- 轮廓,是连接具有相同颜色或强度的所有连续点(沿边界)的曲线。轮廓是用于形状分析以及对象检测和识别的有用工具。
- 为了找到轮廓,通常应用阈值或Canny边缘检测。
查找轮廓
findContours(image, mode, method):从黑色背景中找到白色物体的轮廓。image:仅接受二值图。mode:轮廓检索模式。cv2.RETR_EXTERNAL:表示只检测外轮廓。cv2.RETR_LIST:检测的轮廓不建立等级关系。cv2.RETR_CCOMP:建立两个等级的轮廓,上面的一层为外边界,里面的一层为内孔的边界信息。如果内孔内还有一个连通物体,这个物体的边界也在顶层。cv2.RETR_TREE:建立一个等级树结构的轮廓。
method:轮廓近似方法。cv2.CHAIN_APPROX_NONE:存储所有的轮廓点,相邻的两个点的像素位置差不超过1。cv2.CHAIN_APPROX_SIMPLE:压缩水平、垂直、对角线方向的元素,只保留该方向的终点坐标,例如一个矩形轮廓只需4个点来保存轮廓信息cv2.CHAIN_APPROX_TC89_L1/CV_CHAIN_APPROX_TC89_KCOS:使用 teh-Chinl chain 近似算法
contours:返回的第一个值,图像中所有轮廓组成的list。- 每个轮廓的类型为
ndarray,本质是轮廓上的点的集合。
- 每个轮廓的类型为
hierarchy:返回的第二个可选值,是一个ndarray,其元素个数和轮廓个数相同。- 每个轮廓
contours[i]对应4个轮廓层级属性hierarchy[i][0] ~ hierarchy[i][3],分别表示后一个轮廓、前一个轮廓、父轮廓、内嵌轮廓的索引。如果没有对应项,则该值为负数。
- 每个轮廓
- 在OpenCV中,
findContours()的版本区别:- OpenCV3.2 之前,函数会修改源图像。OpenCV3.2 之后,不再修改源图像。
- OpenCV2 返回两个值:
contours、hierarchy。OpenCV3 返回三个值:img、countours、hierarchy。这里可以用 try-except 解决版本兼容问题。
1 | im = cv2.imread('test.jpg') |
绘制轮廓
cv2.drawContours(image, contours, contourIdx, color, thickness, lineType, hierarchy, maxLevel, offset):绘制任何形状的轮廓。image:指明在哪幅图像上绘制轮廓。contours:轮廓集合。contourIdx:指定绘制轮廓集合中的哪条轮廓,如果是-1,则绘制其中的所有轮廓。thickness:表明轮廓线的宽度,如果是-1(cv2.FILLED),则为填充。
在图像中绘制所有轮廓:
1
cv2.drawContours(img, contours, -1, (0, 255, 0), 3)
绘制单个轮廓,如第四个轮廓:
1
2
3
4cv2.drawContours(img, contours, 3, (0, 255, 0), 3)
# 更好用的等价方法
cnt = contours[4]
cv2.drawContours(img, [cnt], 0, (0,255,0), 3)绘制面积最大的轮廓:
1
2
3
4
5
6
7# 找到最大的轮廓
area = []
for k in range(len(contours)):
area.append(cv2.contourArea(contours[k]))
max_idx = np.argmax(np.array(area))
cnt = contours[max_idx]
cv2.drawContours(img, [cnt], 0, (0,255,0), 3)
轮廓特征
特征矩
- 特征矩可以帮助计算目标的特征,例如物体的质心、面积等。
cv2.moments():提供所有计算出的矩值字典。
1 | img = cv2.imread('test.jpg', 0) |
- 计算质心:
1 | cx = int(M['m10'] / M['m00']) |
轮廓面积
cv2.contourArea(curve):轮廓面积,等价于矩M['m00']。
1 | area = cv2.contourArea(cnt) |
轮廓周长
cv2.arcLength(curve, closed):轮廓弧长。closed:True指定形状是闭合轮廓,False为曲线。
1 | perimeter = cv2.arcLength(cnt, closed=True) |
轮廓凹凸状况
轮廓近似
- 例如试图在图像中找到一个正方形,但是由于图像问题,没能得到一个完美的正方形,则可以近似形状。
cv2.approxPolyDP(curve, epsilon, closed):根据指定的精度,将轮廓形状近似为顶点数量较少的其他形状。由Douglas-Peucker算法实现。epsilon:是一个精度参数,表示从轮廓到近似轮廓的最大距离。需要正确选择epsilon才能获得正确的输出。closed:指定曲线是否闭合。
1 | epsilon = 0.3 * cv2.arcLength(cnt, True) |
在第二张图片中,绿线显示了
ε=周长×10%时的近似曲线。第三张图中,显示了ε=周长×1%时的情况。
轮廓凸包
凸包与轮廓逼近相似,在某些情况下两者可能提供相同的结果。
cv2.convexHull(points, hull, clockwise, returnPoints):检查曲线是否存在凸凹缺陷并进行校正。points:传入轮廓点集。hull:输出,通常不需要。clockwise:方向标志。True表示输出的凸包是顺时针方向的,否则为逆时针。returnPoints:默认值为True。返回凸包点的(x, y)坐标。如果设置为 False,则返回凸包点在轮廓中相应的索引。
1 | hull = cv2.convexHull(cnt) |
检查凸度
cv2.isContourConvex(point):检查曲线是否凸出。只返回True或False。
1 | k = cv2.isContourConvex(cnt) |
凸性缺陷
- 凸包的任何偏差都可以被认为是凸性缺陷。
cv2.convexityDefects():查找凸性缺陷。- 在寻找凸包时,对
cv2.convexHull(points, returnPoints)必须传递returnPoints=False。 - 返回一个数组,其中每行包含这些值:**[起点、终点、最远点、到最远点的近似距离]**。
- 该函数返回的前三个值是cnt的索引。
- 在寻找凸包时,对
1 | import cv2 |
点多边形测试
cv2.pointPolygonTest(contour, pt, measureDist):计算图像中某一点到轮廓线的最短距离。measureDist:如果不想找到距离,则设置为False,因为设置为False可使速度提高2-3倍。True:计算有符号距离。点在轮廓线外时为负数,点在轮廓线内时为正数,点在轮廓线上时为零。False:判断该点是在轮廓线外部还是内部。点在轮廓线外时为-1,点在轮廓线内时为+1,点在轮廓线上时为0。
1 | dist = cv2.pointPolygonTest(contour=cnt, pt=(50, 50), measureDist=True) # 检查(50, 50)到轮廓线的最短距离 |
形状匹配
cv2.matchShapes():比较两个形状或两个轮廓,返回一个显示相似性的度量。结果越低,匹配越好。
1 | import cv2 |
在以下案例中:匹配图像A与本身=0.0;匹配图像A与图像B=0.001946;匹配图像A与图像C=0.326911。

即使是图像旋转也不会对这个比较产生很大的影响。
拟合轮廓
直角矩形
cv2.boundingRect(points):不考虑物体旋转,拟合最小矩形框。注意,其面积不是最小的。points:目标轮廓的点集。(x,y)为矩形的左上角坐标,而(w,h)为矩形的宽度和高度。
1 | x, y, w, h = cv2.boundingRect(cnt) |
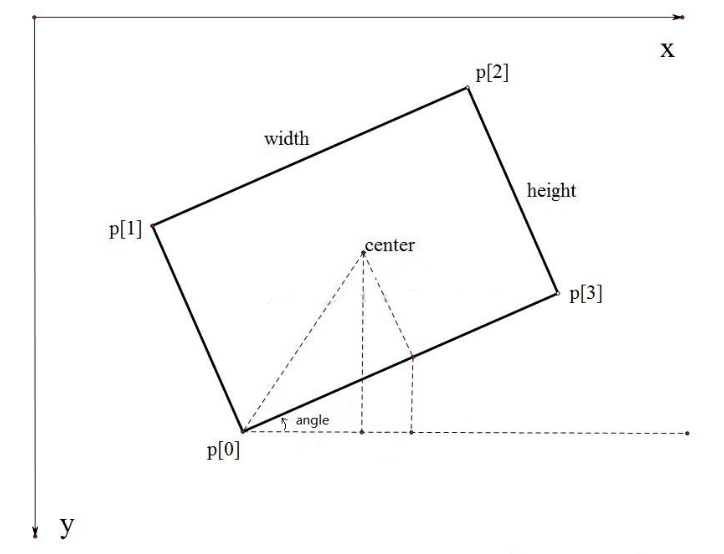
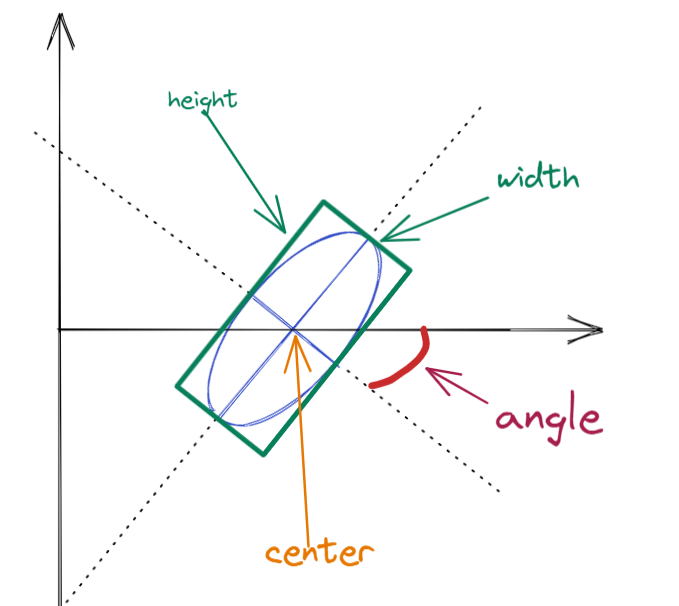
旋转矩形
cv2.minAreaRect(point):考虑旋转,拟合面积最小的外接矩形。point:目标轮廓的点集。- 返回一个Box2D结构:
(中心坐标(x, y), (宽, 高), 旋转角度)。
- cv2.boxPoints():
(中心坐标(x, y), (宽, 高), 旋转角度)->[[x, y] * 4]- 注意版本区别:OpenCV2中为
cv2.cv.BoxPoints,OpenCV3中为cv2.boxPoints()。同样可以用 try-except 兼容版本问题。
- 注意版本区别:OpenCV2中为
1 | rect = cv2.minAreaRect(cnt) |
最小闭合圈
cv2.minEnclosingCircle(point):拟合最小外接圆。
1 | (x, y), radius = cv2.minEnclosingCircle(cnt) |
拟合椭圆
cv2.fitEllipse(point):内接椭圆的旋转矩形。- 很多时候效果并不是非常理想,并没有做到外接。
- 需要5个点以上才能拟合椭圆,否则只能用圆形。
1 | ellipse = cv2.fitEllipse(cnt) |
拟合直线
cv2.fitLine(points, distType, param, reps, aeps):在一组点集上近似一条直线。- 也没啥用。
1 | rows, cols = img.shape[:2] |
轮廓性质
长宽比
- 长宽比:对象边界矩形的宽高比。
1 | x, y, w, h = cv2.boundingRect(cnt) |
范围
- 范围:轮廓区域与边界矩形区域的比值。
1 | area = cv2.contourArea(cnt) |
坚实度
- 坚实度:等高线面积与其凸包面积之比。
1 | area = cv2.contourArea(cnt) |
等效直径
- 等效直径:面积与轮廓面积相同的圆的直径。
1 | area = cv2.contourArea(cnt) |
取向
- 取向:物体指向的角度。
1 | (x, y), (MA, ma), angle = cv2.fitEllipse(cnt) |
掩码
- 掩码:构成该对象的所有点。
- Numpy给出的坐标是
(行、列)格式,而OpenCV给出的坐标是(x,y)格式。注意,row = x, column = y。
1 | mask = np.zeros(imgray.shape, np.uint8) |
最大值、最小值及其位置
- 可以使用掩码图像找到这些参数。
1 | min_val, max_val, min_loc, max_loc = cv2.minMaxLoc(imgray, mask=mask) |
平均颜色、平均强度
- 找到对象的平均颜色,或者灰度模式下物体的平均强度。
1 | mean_val = cv2.mean(img, mask=mask) |
极端点
- 极端点:指对象的最顶部,最底部,最右侧和最左侧的点。
1 | leftmost = tuple(cnt[cnt[:, :, 0].argmin()][0]) |