PyTorch深度学习实践Part4——反向传播

对于简单模型可以手动求解析式，但是对于复杂模型求解析式几乎不可能。

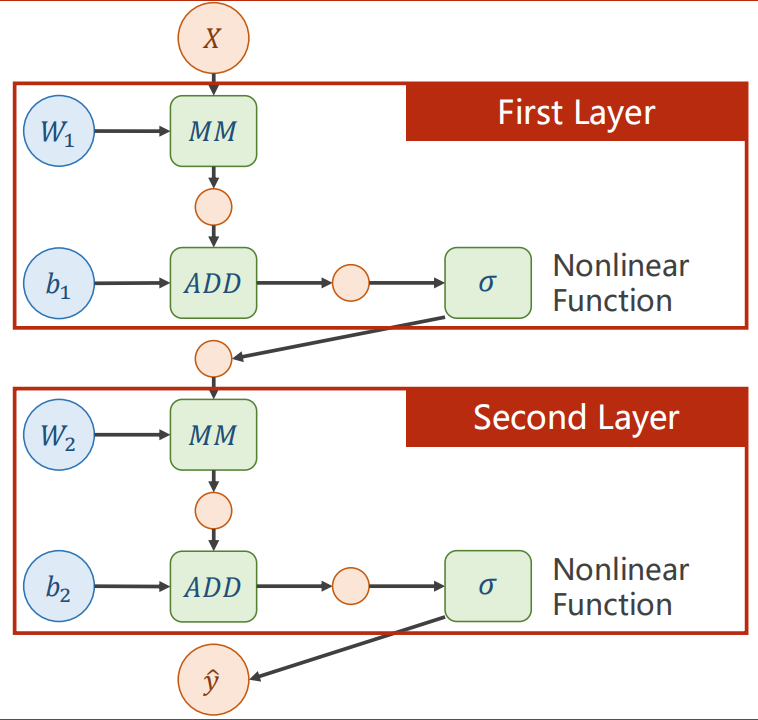
计算图

每一层神经网络包括一次矩阵乘法(Matrix Multiplication)、一次向量加法、非线性变化函数(为了防止展开函数而导致深层神经网络无意义)

image-20210116225529823

链式法则

在pytorch中，梯度存在变量而不是计算模块里。

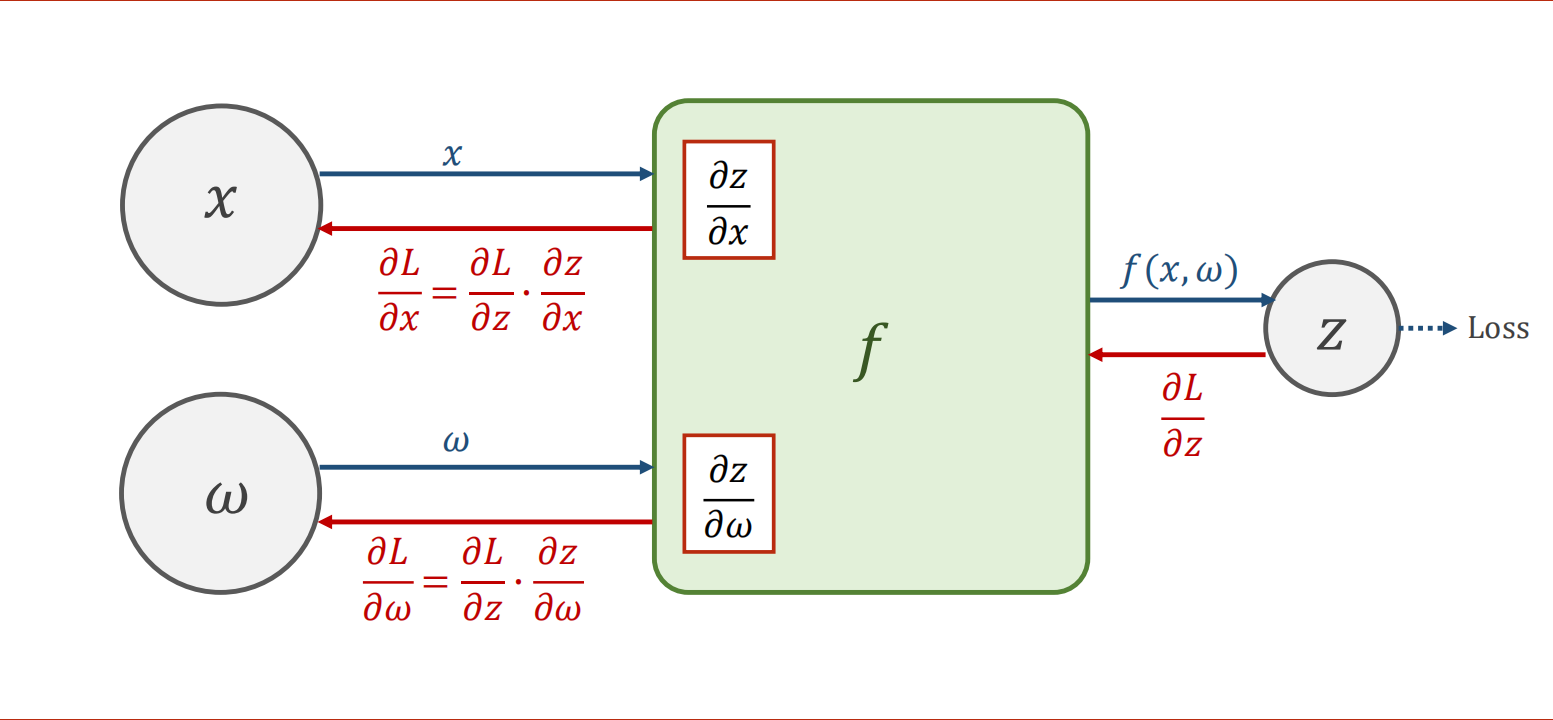
image-20210116230629292

image-20210117091957454

在计算过程中中，虽然有些变量可以不求导，但是一样要具备能够求导的能力。比如x的值就有可能是前一层网络的y_hat传递下来的。

核心在于梯度，loss虽然不会作为变量参与计算过程，但是同样需要保留，作为图像数据来判断最终是否收敛。

PyTorch实现反向传播

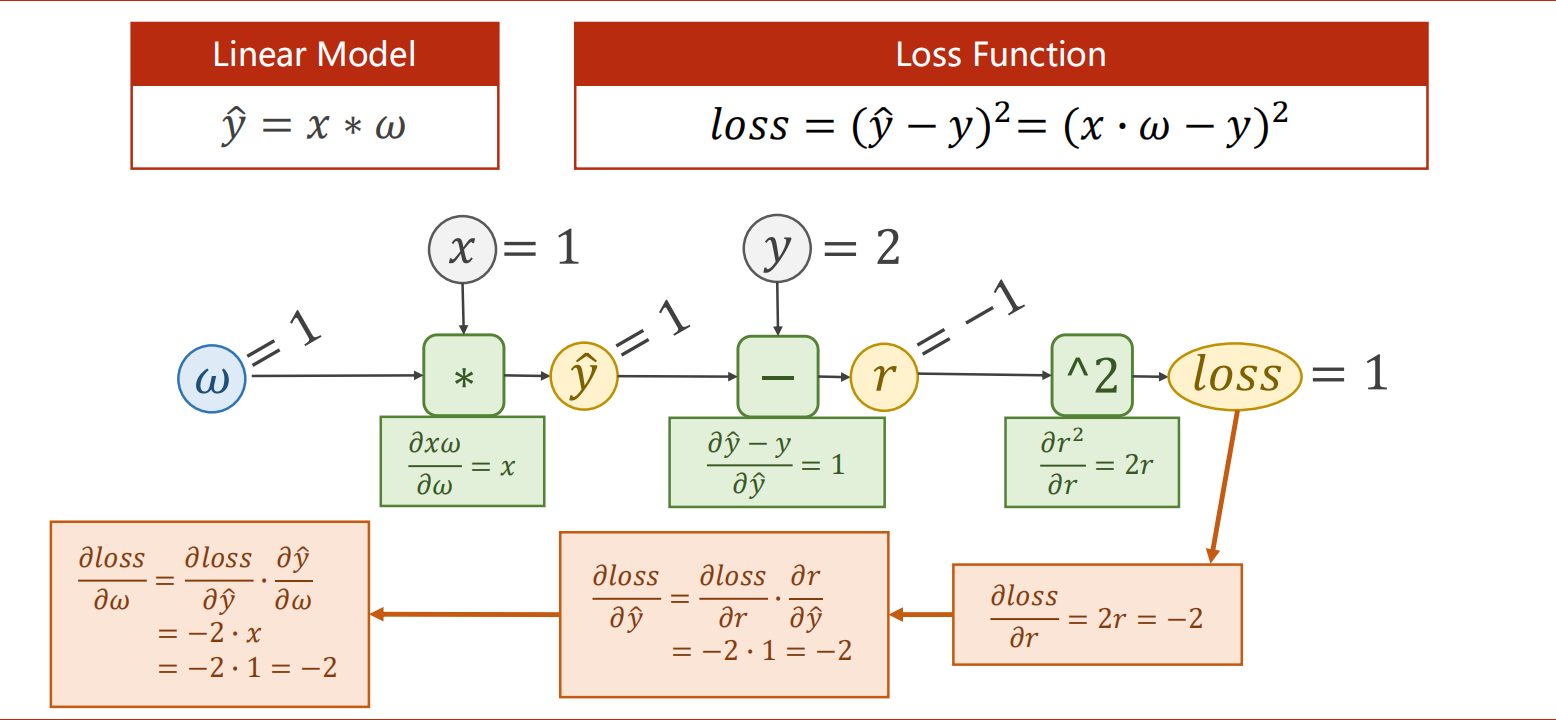
线性模型y=w*x，用pytorch实现反向传播

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import torch

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = torch.Tensor([1.0])  # data必须是一个序列
w.requires_grad = True  # 需要计算梯度


def forward(x):
    return x * w  # w是Tensor，运算符重载，x也会转成tensor


def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2  # 看到代码一定要有意识想到如何构建计算图


print("predict (before training)", 4, forward(4).item())

for epoch in range(100):
    for x, y in zip(x_data, y_data):
        l = loss(x, y)  # 前馈过程，正式构建计算图，计算损失更新l
        l.backward()  # 反向传播，计算梯度，释放计算图
        print('\tgrad:', x, y, w.grad.item())
        w.data = w.data - 0.01 * w.grad.data  # 更新权重w，注意grad也是一个tensor，不使用.data的话相当于在构建计算图

        w.grad.data.zero_()  # 将梯度w.grad.data清零

    print('progress:', epoch, l.item())  # 取出loss使用l.item，不要直接使用l（l是tensor会构建计算图）

print("predict (after training)", 4, forward(4).item())
# predict (after training) 4 7.999998569488525

课后作业

二次模型y=w1x²+w2x+b的反向传播

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import torch

# y = x ** 2 + 2 * x + 1
x_data = [1.0, 2.0, 3.0]
y_data = [4.0, 9.0, 16.0]

w1 = torch.Tensor([1.0])
w2 = torch.Tensor([1.0])
b = torch.Tensor([1.0])
w1.requires_grad, w2.requires_grad, b.requires_grad = True, True, True


def forward(x):
    return w1 * x * x + w2 * x + b


def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2


print("predict (before training)", 4, forward(4).item())

for epoch in range(100):
    for x, y in zip(x_data, y_data):
        l = loss(x, y)  # 前馈过程，正式构建计算图，计算损失更新l
        l.backward()  # 反向传播，计算梯度，释放计算图
        print('\tgrad:', x, y, w1.grad.item(), w2.grad.item(), b.grad.item())
        w1.data = w1.data - 0.01 * w1.grad.data
        w2.data = w2.data - 0.01 * w2.grad.data
        b.data = b.data - 0.01 * b.grad.data
        w1.grad.data.zero_()
        w2.grad.data.zero_()
        b.grad.data.zero_()
    print('progress:', epoch, l.item())  # 取出loss使用l.item，不要直接使用l（l是tensor会构建计算图）

print("predict (after training)", 4, forward(4).item())
print(w1.data, w2.data, b.data)
# predict (after training) 4 25.259323120117188
# tensor([1.1145]) tensor([1.4928]) tensor([1.4557])

改了一下原本的数据集，更符合二次函数，但是因为样本量过少，预测的权重并不是很好。