PyTorch深度学习实践Part2——线性模型

一般过程

  1. Data Set
  2. Model（神经网络、决策树、朴素贝叶斯）
  3. Trainning
  4. Infering

训练&测试

训练集拆分

在竞赛中，训练集是可见的，测试集一般是不可见的。为了提高或验证模型的准确度，一般会把手中的训练集拆分，以及交叉验证。

过拟合

当模型对训练集的噪声也学习进去的时候，对训练集以外的数据可能会出现准确率下降的情况。因此一个好的模型需要有良好的泛化能力。

损失函数

image-20210116101533492

平均平方误差（MSE MeanSquareError）

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]


# 前馈
def forward(x):
    return x * w


# 损失
def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) * (y_pred - y)


# 存放结果，所有权重和对应的均方差
w_list = []
mse_list = []
# 穷举所有权重0.0-4.1步长0.1
for w in np.arange(0.0, 4.1, 0.1):
    print('w=', w)
    l_sum = 0  # 损失的和
    for x_val, y_val in zip(x_data, y_data):  # 打包，一共三行
        y_pred_val = forward(x_val)  # 前馈算出此权重和样本得出的预测值，其实已经包含在loss()中，只是为了打印
        loss_val = loss(x_val, y_val)  # 计算该权重预测值得损失
        l_sum += loss_val  # 求损失和
        print('\t', x_val, y_val, y_pred_val, loss_val)  # 当前的x、y值、预测值、损失
    print('MSE=', l_sum / 3)  # 求损失的平均
    # 保存记录
    w_list.append(w)
    mse_list.append(l_sum / 3)
# 图表打印
plt.plot(w_list, mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()

image-20210116155722125

做深度学习要定期存盘，防止意外导致数据丢失

课后作业

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
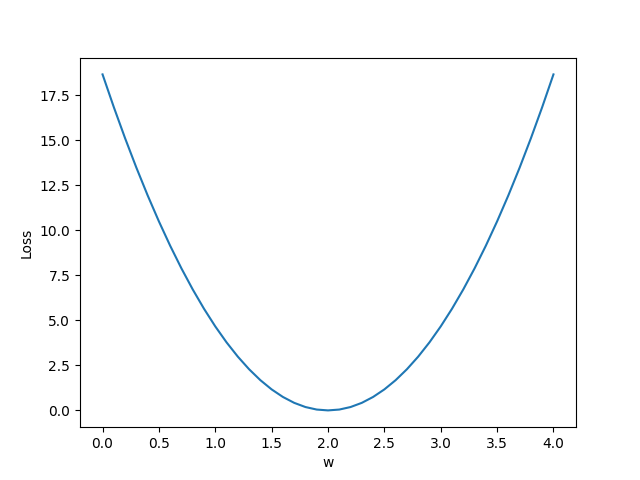
import numpy as np
import matplotlib.pyplot as plt

# 这里设函数为y=3x+2
x_data = [1.0, 2.0, 3.0]
y_data = [5.0, 8.0, 11.0]


def forward(x):
    return x * w + b


def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) * (y_pred - y)


# 1.arange()左闭右开；2.打印 0.0、1.0 时只会显示 0.、1.；3.meshgrid()之后w、b都是41*41矩阵
# 4.这里前馈中是矩阵点对点的运算，但注意并不是矩阵运算，好处是省去了n层for循环，举例：
# a=[[1 2 3][1 2 3]]
# b=[[7 7 7][8 8 8]]
# a*b=[[ 7 14 21][ 8 16 24]]
w_list = np.arange(0.0, 4.1, 0.1)
b_list = np.arange(0.0, 4.1, 0.1)
w, b = np.meshgrid(w_list, b_list)

l_sum = 0  # 损失的和
for x_val, y_val in zip(x_data, y_data):  # 遍历三次
    # y_pred_val、loss_val都是41*41的矩阵，即41个w和41个b组合的预测结果和损失
    y_pred_val = forward(x_val)
    loss_val = loss(x_val, y_val)
    l_sum += loss_val
    print('\nx_val：', x_val,'\ny_val：', y_val, '\ny_pred_val：',y_pred_val, '\nloss_val：',loss_val)  # 当前的x、y值、预测值、损失
mse_list = l_sum / 3
# mse_list也是一个ndarray类型的41*41矩阵
print('MSE=', mse_list)

# 3d图表
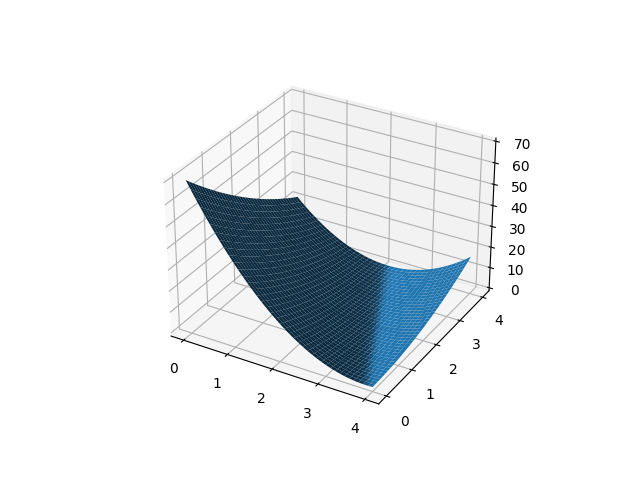
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(w, b, mse_list)
plt.show()
import numpy as np
import matplotlib.pyplot as plt

# 这里设函数为y=3x+2
x_data = [1.0, 2.0, 3.0]
y_data = [5.0, 8.0, 11.0]


def forward(x):
    return x * w + b


def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) * (y_pred - y)


# 这里都是矩阵的运算
# 1.arange()左闭右开；2.打印 0.0、1.0 时只会显示 0.、1.；3.meshgrid之后w、b都是41*41矩阵
w_list = np.arange(0.0, 4.1, 0.1)
b_list = np.arange(0.0, 4.1, 0.1)
w, b = np.meshgrid(w_list, b_list)

l_sum = 0  # 损失的和
for x_val, y_val in zip(x_data, y_data):  # 遍历三次
    y_pred_val = forward(x_val)
    loss_val = loss(x_val, y_val)
    l_sum += loss_val
    print('\nx_val：', x_val,'\ny_val：', y_val, '\ny_pred_val：',y_pred_val, '\nloss_val：',loss_val)  # 当前的x、y值、预测值、损失
mse_list = l_sum / 3
# mse_list也是一个ndarray类型的41*41矩阵
print('MSE=', mse_list)

# 3d图表
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(w, b, mse_list)
plt.show()

image-20210116155626917