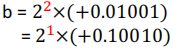计算机组成原理-Part2——数据的表示和运算

[TOC]

数制与编码

进位计数制及其相互转换

r 进制计数法

  • 基数：每个数码位所用到的不同符号的个数，r 进制的基数为 r
  • 位权：处于第 i 位的权重，值为 r^i^
  • 每个位上的取值范围：0 ~ r-1

其他进制 -> 十进制

  • r 进制数：KnKn-1……K1K0K-1……K-m
  • 十进制： Kn × r^n^ + Kn-1 × r^n-1^ + …… + K1 × r^1^ + K0 × r^0^ + K-1 × r^-1^ + …… + K-m × r^m^
2^12^ 2^11^ 2^10^ 2^9^ 2^8^ 2^7^ 2^6^ 2^5^ 2^4^ 2^3^ 2^2^ 2^1^ 2^0^ 2^-1^ 2^-2^ 2^-3^
4096 2048 1024 512 256 128 64 32 16 8 4 2 1 0.5 0.25 0.125

二、八、十六进制之间相互转换

  • image-20211003084155324
  • 各种进制的常见书写方式
    • 二进制（Binary）：(1010001010010)2 或 1010001010010B
    • 八进制：(1652)8
    • 十六进制（hex）：(1652)16 或 1652H 或 0x1652
    • 十进制（dec）：(1652)10 或 1652D
  • 注意需要补位：整数向前补 0，小数向后补 0。

十进制 -> 其他进制

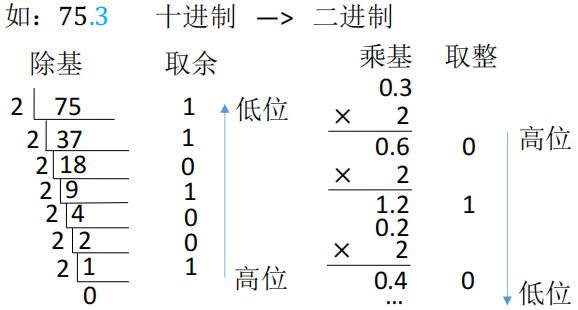
  • image-20211003085557768
  • 整数部分除法：先除得的余数为低位（靠近0）
  • 小数部分乘法：先进位的整数为高位（靠近0）
  • 也可以使用拼凑法：枚举 r 进制数与十进制数的对应表
  • 有的十进制小数无法使用二进制精确表示，如：0.3

真值和机器数

  • 真值：符合人类习惯的数字
  • 机器数：数字实际存到机器里的形式，正负号需要被“数字化”

BCD码（408大纲已删）

  • BCD ：Binary-Coded Decimal，用二进制编码的十进制
    • 8421 码（掌握加法）
    • 余 3 码
    • 2421 码
  • 针对问题：二进制方便计算机处理、十进制符合人类习惯，但是转换麻烦
  • 改进方向：快速转换，一一对应
  • 以 4bit 二进制码表示 0~9。一共 16 种情况，6 种冗余。

8421 码

  • 4 位二进制权值分别为：8 4 2 1
  • 8421 码是有权码
  • 8421 码的加法：先用十进制加法得出结果，再转 8421 码
  • 8421码中，1010～1111 没有定义
  • 在机器的视角中，若发现结果非法定义（6+7）或出现进位（9+9），则需要继续 +6 进行修正。
0 1 2 3 4 5 6 7 8 9
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001

余 3 码

  • 余3码：8421码 + (0011)2
  • 余 3 码的每个权位不固定，所以是无权码
0 1 2 3 4 5 6 7 8 9
0011 0100 0101 0110 0111 1000 1001 1010 1011 1100

2421 码

  • 4 位二进制权值分别为：2 4 2 1
  • 04 首位必须是 0，59 首位必须是 1
0 1 2 3 4 5 6 7 8 9
0000 0001 0010 0011 0100 1011 1100 1101 1110 1111

字符与字符串

ASCII 码

  • 键盘共 128 个字符，可以用 7 位二进制编码。
    • 为了存入计算机，通常在最高位补 0，凑足1B
  • 可印刷字符：32～126，其余为控制（如：127 DEL）、通信（如：6 ACK）字符
  • 数字 0~9：48(0011 0000)～57(0011 1001)
    • 数字的 ASCII 码的前四位是 0011，后四位是 8421 码
  • 大写字母 A~Z：65(0100 0001)～90(0101 1010)
    • 大写字母 ASCII 码前三位都是 010，后五位是 1~26
  • 小写字母 a~z：97(0110 0001)～122(0111 1010)
    • 小写字母 ASCII 码前三位都是 011，后五位是 1~26
  • 所有数字、大写字母、小写字母的编码都是连续的

求解某字符 ASCII 码时，要充分利用上述规律，避免十进制、二进制转换。

汉字的表示和编码

  • GB 2312-100（19100年）：汉字+各种符号共7445个
  • 区位码：94 个区，每区 94 个位置。相当于把所有汉字存放在了 94*94 的方阵中，通过两个字节长度来定位汉字
  • 国标码：区位码 + 20H。防止信息交换时与“控制/通信字符”冲突
  • 汉字(机)内码：国标码 + 100H。保证高位为1，与ASCII码区分
  • 输入法 -> 国标码 -> 汉字内码 -> (国标码 -> )汉字字形码（像素方阵）

字符串

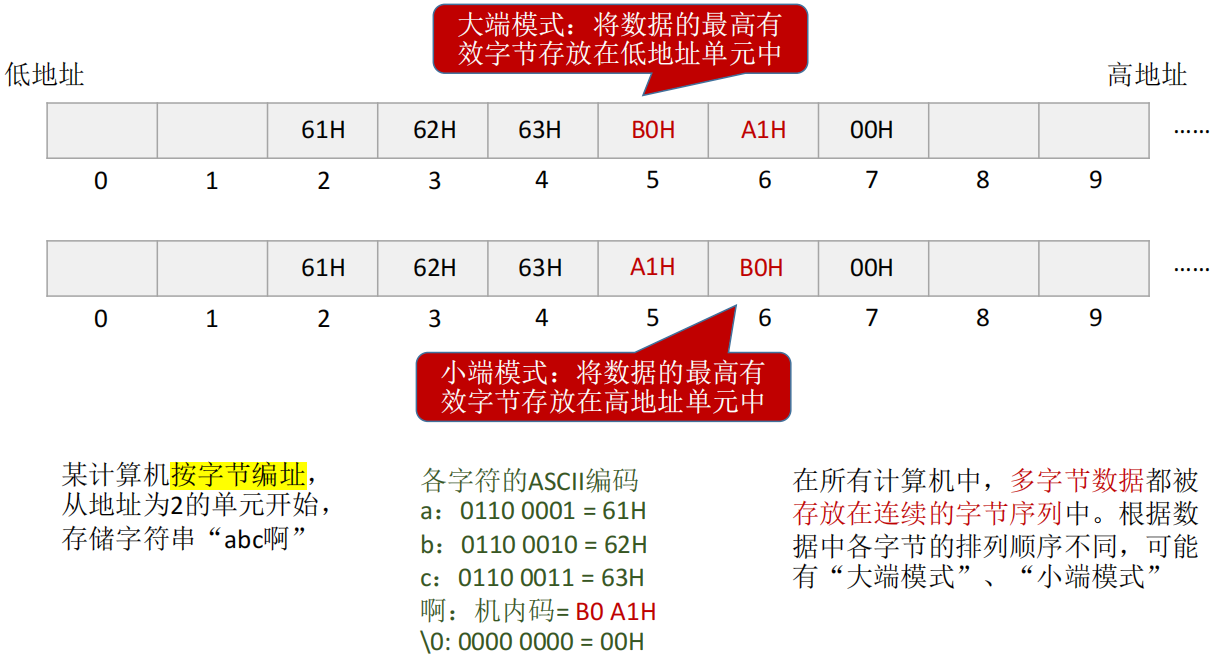
  • image-20211003101235176
  • 按字节编址：每个地址对应 1B/1字节（存储单元大小为 1B/8b）
  • 很多语言中，“\0”作为字符串结尾标志
  • 在所有计算机中，多字节数据都被存放在连续的字节序列中。根据数据中各字节的排列顺序不同，可能有“大端模式”、“小端模式”
    • 大端模式：将数据的最高有效字节存放在低地址单元中（低位到高位顺序读取）
    • 小端模式：将数据的最高有效字节存放在高地址单元中（遇到多字节数据需要倒着读）

奇偶校验码（计网要考）

校验原理

  • 位错误：在 bit 位上发生的突变。0 变 1，1 变 0
  • 码字：由若干位代码组成的一个字
  • 两个码字间的距离：将两个码字逐位进行对比，具有不同的位的个数
  • 码距：一种编码方案中，合法码字之间的最小距离。最少变动多少位可以在各合法码字之间转换
  • 当 d=1 时，无检错能力；当 d=2 时，有检错能力；当 d≥3 时，若设计合理，可能具有检错、纠错能力

奇偶校验码

  • image-20211004142023267
  • 奇校验码：在有效信息位之外添加一位校验位，使得整个校验码中“1”的个数为奇数。
  • 偶校验码：在有效信息位之外添加一位校验位，使得整个校验码中“1”的个数为偶数。
  • 本质：如果出现奇数次的位错误，则可以检测出错误；如果出现偶数次位错误，则检不出错误。
  • 偶校验的硬件实现：取各位的信息依次进行异或（模2加）运算，得到的结果即为偶校验位。
    • 进行偶校验且结果为 0 时，则通过校验。
    • 进行奇校验且结果为 1 时，则通过校验。
  • image-20211004143356036

海明校验码（计网要考）

基本思想

  • 针对问题：偶校验只能发现奇数位错误，且无法确定出错位置，想要获得正确信息则必须重新传输信息。
  • 改进方向：将信息位分组进行偶校验 —> 多个校验位 —> 多个校验位标注出错位置
    • 1 个校验位之只能携带 2 种状态信息（对/错）
    • 多个校验位能携带多种状态信息（对/错，错在哪）
  • 信息位 n 位 + 校验位 k 位 = 共 n+k 位
    • k 位校验位代表最多能表示 2^k^ 种状态
    • 校验位表示的状态应该要考虑到 n+k 的任何一位都有可能出错
    • 重要公式：2^k^ ≥ n + k + 1
  • 本质：分 k 组偶校验

海明码求解步骤（TODO）

Eg：信息位为 1010，求解海明码。

  1. 确定海明码的位数：

    • 2^k^ ≥ n + k + 1
    • n=4 => k=3

  2. 确定校验位的分布：

    • 设信息位 D4D3D2D1（1010），共4位；校验位 P3P2P1，共3位；对应的海明码为 H7H6H5H4H3H2H1

    • 校验位 Pi 放在海明位号为 2^i−1^ 的位置上

    • 校验位 Pi 与位置序号第 i 位为 1 的信息位归为同一组，进行偶校验

    • H7 H6 H5 H4 H3 H2 H1
      D4 D3 D2 P3 D1 P2 P1
      1 0 1 0 0 1 0

  3. 求校验位的值：

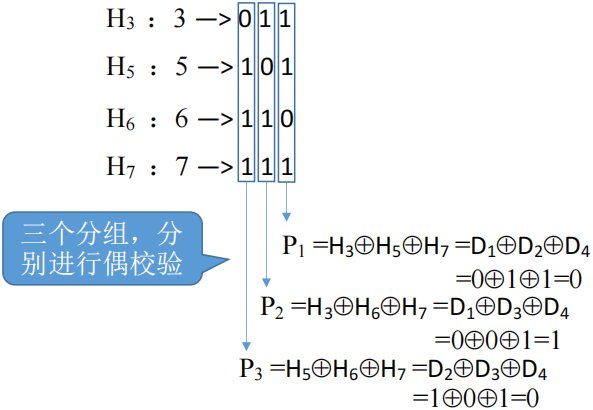
    • image-20211004151532962
    • 将海明码信息位的下标转二进制矩阵，一列为一组，对应 1 的信息拿出来做偶校验，结果就是海明码校验位的值。

  4. 纠错：

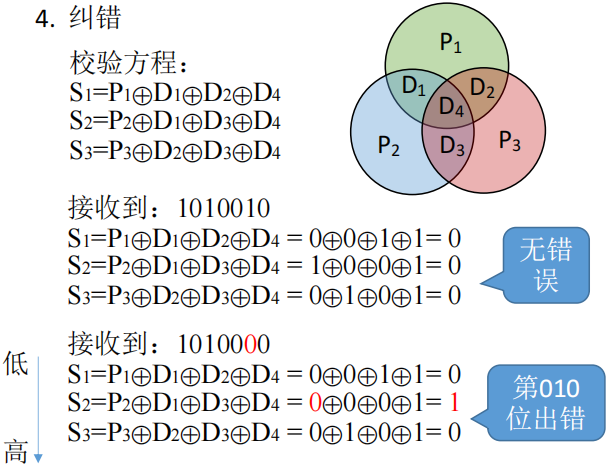
    • image-20211004154938467
    • 题目的下标顺序不影响做题（TODO）

海明码的检错、纠错能力

  • 海明码的检错、纠错能力：
    • 纠错能力：1位（无法区分到底是 1 位错还是 2 位错）
    • 检错能力：2位
  • 为了区分是 1 位错误还是 2 位错误，需加上“全校验位”，对整体进行偶校验。
  • image-20211004155557262

循环冗余校验码（计网要考）

基本思想

  • 循环冗余校验（Cyclic Redundancy Check，CRC）
  • 数据发送、接受方共同约定一个“除数”
  • K个信息位+R个校验位 作为“被除数”，添加校验位以保证除法的余数为 0
    • 收到数据后，进行除法检查余数是否为0
    • 若余数非 0 说明出错，则进行重传或纠错

构造、检错、纠错

  • image-20211004164514722
  • 流程：
    1. 题目给出生成多项式、信息码
    2. K = 信息码的长度 = 6，R = 生成多项式最高次幂 = 3 => 校验码位数 N = K + R = 9
    3. 信息码左移 R 位，低位补 0。利用生成多项式系数进行模2除法，得余数为校验码。
    4. 将接受到的码字用生成多项式进行模2除法，余数为000则代表没有出错，否则不然。
  • 循环冗余校验码的检错、纠错特性：
    • 可检测出所有奇数个错误
    • 可检测出所有双比特的错误
    • 可检测出所有小于等于校验位长度的连续错误
    • 对于确定的生成多项式，出错位与余数是相对应的
    • 当码字长度超出检错码可表示的能力时，出错位与余数的对应关系将进行循环
    • K个信息位，R个校验位，若生成多项式选择得当，且 2^R^≥K+R+1，则 CRC 码可纠正1位错

定点数的表示与运算

  • 定点数：小数点的位置固定（定点数也包含小数）
    • 常规计数
    • Eg：996.007
  • 浮点数：小数点的位置不固定
    • 科学计数法
    • Eg：9.96007*102

定点数的表示

无符号数的定点表示

  • 无符号数：整个机器字长的全部二进制位均为数值位，没有符号位，相当于数的绝对值。
  • 通常只有无符号整数，而没有无符号小数（unsigned int/long）
  • 表示范围：n 位 bit 的无符号数表示范围为：0 ～ 2n-1
    • Eg：8位二进制数： 2^8^ 种不同的状态，表示 0000 0000 ～ 1111 1111，即 0 ~ 255

有符号数的定点表示

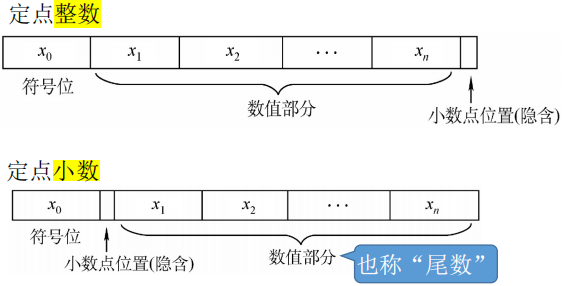
  • image-20211007120237263
  • 可用 原码、反码、补码 三种方式来表示定点整数和定点小数。还可用 移码 表示定点整数。
  • 若真值为 x，则用 [x]原、[x]反、[x]补、[x]移 分别表示真值所对应的原码、反码、补码、移码
  • 若机器字长为 n+1 位，则符号位占 1 位，尾数占 n 位
  • 表示定点整数，默认小数点隐含在尾数后；表示定点小数，默认小数点隐含在符号位后尾数前。
原码表示定点整数和定点小数
  • image-20211007121910742
  • 未指明机器字长时，整数尾数前端的 0 可略去，小数尾数后端的 0 可略去。
  • 要注意第一位是符号位，切不能当成数值。
  • 整数原码常用 逗号 分割符号位和尾数，小数原码常用 小数点 分割符号位和尾数。
  • image-20211007123125347
  • 在整数和小数的原码表示中，真值 0 有 +0 和 -0 两种形式，即两种二进制状态对应了同一种真值。
    • 因此即使机器字长为 n+1 位，理论上能够表示 2^n+1^ 种情况，但实际上值表示了 2^n+1^-1 种。
  • 原码整数表示范围：**-(2^n^-1)≤x≤2^n^-1；源码小数表示范围：-(1-2^n^)≤x≤1-2^n^**。
反码表示定点整数和定点小数
  • image-20211007124524338
  • 反码：若符号位为0，则反码与原码相同；若符号位为1，则数值位全部取反。
  • 表示范围和源码相同。

“反码”只是“原码”转变为“补码”的一个中间状态，实际中并没什么卵用——并没有解决“真值 0 有 +0 和 -0 两种形式”这个问题。

补码表示定点整数和定点小数
  • image-20211007131951644
  • 补码：正数的补码=原码；负数的补码=反码末位+1（要考虑进位）
  • 补码的真值 0 只有一种表示形式：[+0]补= [-0]补= 00000000
    • 定点整数
      • [-2^7^]补 = **1,**0000000
      • 表示范围：−2^n^ ≤ x ≤ 2^n^−1
    • 定点小数
      • [-1]补 = **1.**0000000
      • 表示范围：-1 ≤ x ≤ 1-2^-n^
  • 由 [x]补 快速求 [-x]补 的方法：符号位、数值位全部取反，末位+1
移码表示定点整数
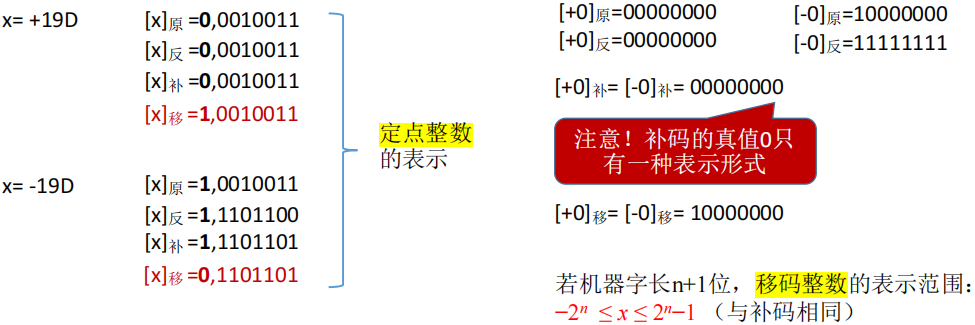
  • image-20211007143059138
  • 移码：补码的基础上将符号位取反。注意：移码只能用于表示整数。
  • 移码表示的整数很方便对比大小
  • 在浮点数中将大量使用移码

原码补码移码的作用

  • 无符号数：可以进行直接加减运算。
  • 原码的加减运算：需要将符号位单独区分，但是这样将增加硬件成本、计算复杂度。
    • 因此需要用加法运算来代替减法运算 => 将减法操作转换成取模运算（例如：-3mod12=9）
  • 补码的本质：为了能够进行直接加运算，将系统设计成了循环。
  • 反码的本质：将原码的负数部分进行了反转，是补码能够循环的铺垫。
  • 移码的本质：使用偏置将补码的循环提前了半个周期。
二进制机器数 二进制表示无符号数 二进制表示原码 二进制表示反码 二进制表示补码 二进制表示移码
0000 0000 0 +0 +0 0 -128
0000 0001 1 1 1 1 -127
…… …… …… …… …… ……
0111 1111 127 127 127 127 -1
1000 0000 128 -0 -127 -128 0
1000 0001 129 -1 -126 -127 1
…… …… …… …… …… ……
1111 1111 255 -127 -0 -1 127
  • 带余除法——设 x, m∈Z, m>0 则存在唯一决定的整数 q 和 r，使得：x = q*m + r , 0 ≤ r < m
    • (mod 12) 把所有整数分为 12 类（余数为 0~11）
    • (mod 12) 余数相同的数，都是同一类，都是等价的
    • 在 (mod m) 的条件下，若能找到负数的补数，就可以用正数的加法来等价替代减法
      • 若二个数绝对值之和=模，则称这两个数互为补数
    • 模 - a的绝对值 = a的补数
    • ↑ 这是补码的原生定义
  • 反码 + 原码 + 1 = 模
  • 补码的作用： 使用补码可将减法操作转变为等价的加法，ALU 中无需集成减法器。执行加法操作时，符号位一起参与运算。

移位运算

算数移位

  • 移位：通过改变各个数码位和小数点的相对位置，从而改变各数码位的位权。可用移位运算实现乘法、除法

  • 原码的算数移位——符号位保持不变，仅对数值位进行移位。

    • 右移：高位补0，低位舍弃。若舍弃的位=0，则相当于÷2；若舍弃的位≠0，则会丢失精度
    • 左移：低位补0，高位舍弃。若舍弃的位=0，则相当于×2；若舍弃的位≠0，则会出现严重误差

  • 反码的算数移位

    • 正数的反码与原码相同，因此对正数反码的移位运算也和原码相同。
      • 右移：高位补0，低位舍弃。
      • 左移：低位补0，高位舍弃。
    • 负数的反码数值位与原码相反，因此负数反码的移位在补位上有所变化。
      • 右移：高位补1，低位舍弃。
      • 左移：低位补1，高位舍弃。

  • 补码的算数移位

    • 正数的补码与原码相同，因此对正数补码的移位运算也和原码相同。
      • 右移：高位补0，低位舍弃。
      • 左移：低位补0，高位舍弃。
    • 负数补码=反码末位+1，导致反码最右边几个连续的1都因进位而变为0，直到进位碰到第一个0为止。
      • 负数补码中：最右边的1及其右边同原码；最右边的1的左边同反码负数补码。
      • 右移（同反码）：高位补1，低位舍弃。
      • 左移（同原码）：低位补0，高位舍弃。
  • image-20211008121454539

  • Eg：-20×7 = -20×(2^0^+2^1^+2^2^) = (-20左移0位) + (-20左移1位) + (-20左移2位)

逻辑移位

  • 逻辑右移：高位补0，低位舍弃。
  • 逻辑左移：低位补0，高位舍弃。
  • 可以把逻辑移位看作是对“无符号数”的算数移位
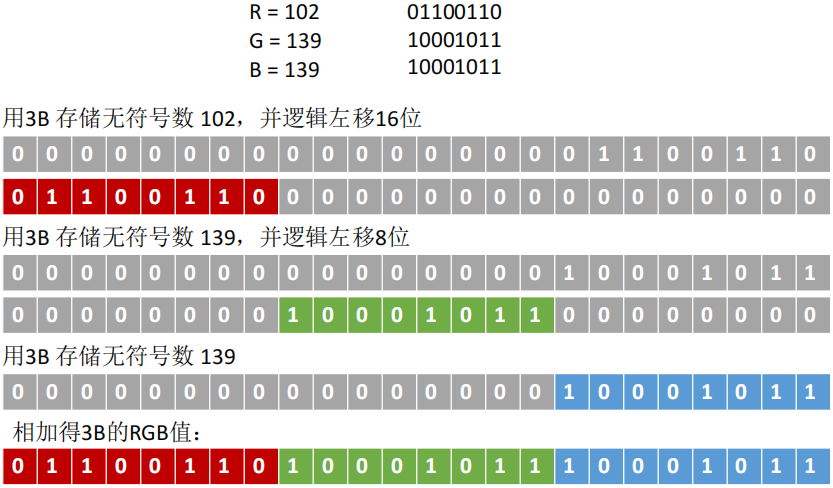
  • Eg：image-20211008122429002

循环移位

  • 不带进位位：用移出的位补上空缺
  • 带进位位：用进位位的值补上空缺，而移出的位放到进位位
  • Eg：交换高低位字节时常用（大端存储<=>小端存储）

加减运算和溢出判断

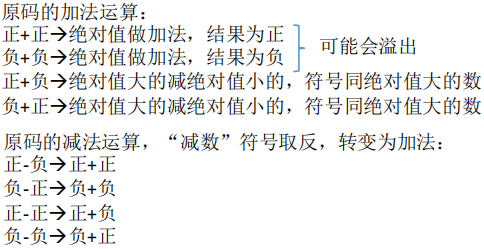
原码的加减法

  • 要考虑 2*2 种情况，并且同时实现加法器和减法器
  • image-20211008124354552

补码的加减法

  • 负数的补码转原码：

    • 数值位取反，+1
    • -1，数值位取反
    • 负数补码中，最右边的1及其右边同原码，最右边的1的左边同反码

  • [(负数)]补 <=> [(负数)]原：取负数补码最右边的一位1，其本身与其右侧不变，左侧数值位全部取反。（常用）

  • [x]补 => [-x]补：连同符号位一起取反加1。

溢出判断

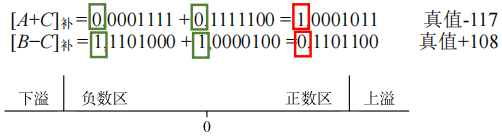
  • image-20211008151859101
  • 溢出情况：
    • 只有“正数+正数 ”才会上溢 —— 正+正=负
    • 只有“负数+负数 ”才会下溢 —— 负+负=正
  • 判断方法：
    • 法一：采用一位符号位设 A 的符号为 AS，B 的符号为 BS，运算结果的符号为 SS，则溢出逻辑表达式为：
      • $V = A_{s}B_{s}\overline{S_{s}} + \overline{A_{s}}\overline{B_{s}}S_{s}$
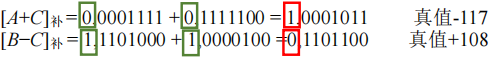
      • image-20211008163931615
      • 若 V=0，表示无溢出；若 V=1，表示有溢出。
      • AS 为 1 且 BS 为 1 且 SS 为 0 或 AS 为 0 且 BS 为 0 且 SS 为 1。
    • 法二：采用一位符号位，根据数据位进位情况判断溢出符号位的进位 CS，最高数值位的进位 C1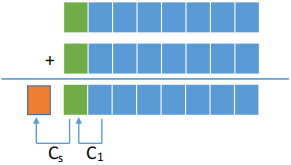
      • image-20211008163814192
      • $V=C_{S}⊕ C_{1}$
      • 若 V=0，表示无溢出；若 V=1，表示有溢出。
      • 最高数值位进位且符号位不进位 或 符号位进位而最高数值位不进位。
    • 法三：
      • 采用双符号位：正数符号为 00，负数符号为 11
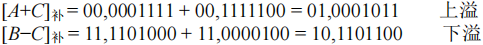
      • image-20211008163848872
      • 记两个符号位为 SS1SS2 ，则 $V=S_{S1}\otimes S_{S2}$。若 V=0，表示无溢出；若 V=1，表示有溢出。
      • 第一个符号位表明应该得到的符号，第二个符号位表明实际得到的符号。
      • 双符号位补码又称：模 4 补码；单符号位补码又称：模 2 补码。
      • 实际存储时只存储一个符号位，运算时会复制一个符号位
  • 同+同=异 => 发生溢出

符号扩展

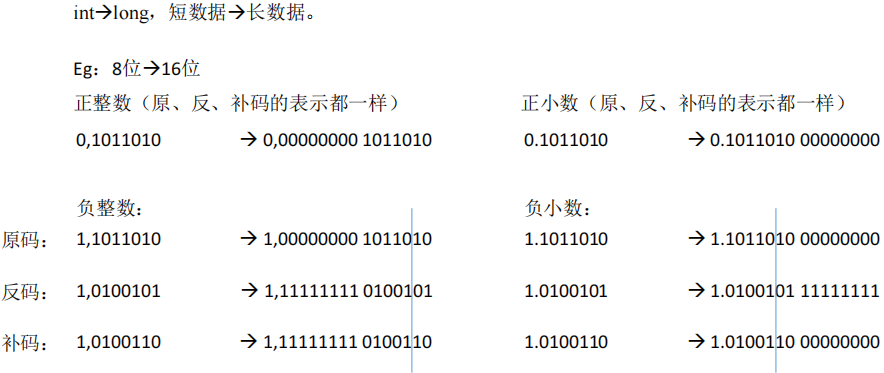
  • image-20211008164330993
  • 定点整数的符号扩展：在原符号位和数值位中间添加新位，正数都添0；负数原码添0，反码、补码添1
  • 定点小数的符号扩展：在原符号位和数值位后面添加新位，正数都添0；负数原码、补码添0，反码添1

乘法运算

乘法运算的实现思想

  • 用移位实现乘数累加
  • Eg：0.1101×0.1011 = (1101×1×2^-8^ ) + (1101×1×2^-7^) + (1101×0×2^-6^) + (1101×1×2^-5^)

原码的一位乘法

  • 符号单独处理：符号位 = xs⊕ys
  • 数值位取绝对值进行乘法计算
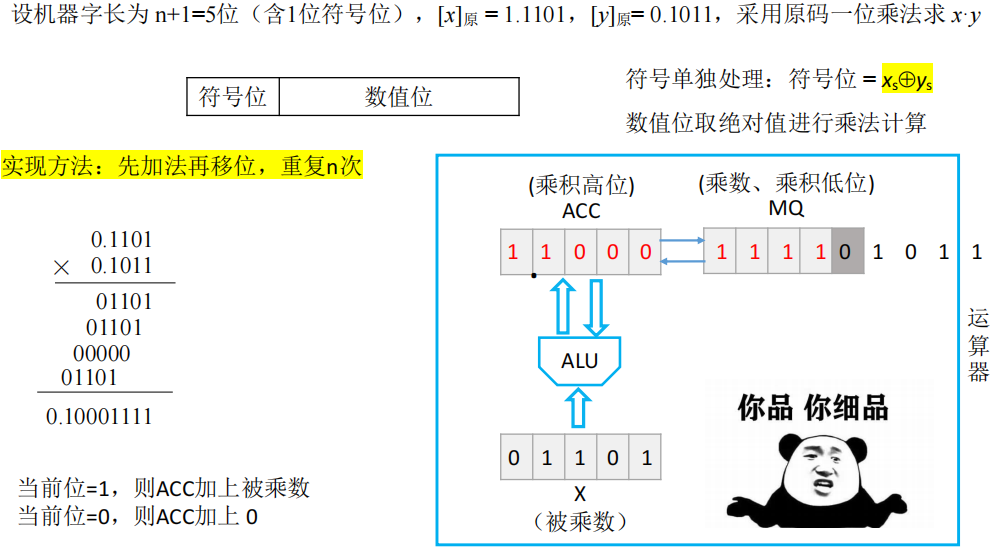
  • image-20211009130101904
  • 在机器实现乘法中：
    • ACC 存放乘积高位，MQ 存放乘数与乘积低位，X 存放被乘数
    • 在正式进行乘法之前，ACC 置零
    • 先将 X 中被乘数与 MQ 最低位的乘积结果加到 ACC 中
    • 再将 ACC、MQ 整体逻辑右移一位
      • 逻辑右移，高位补零
      • ACC 的低位移到 MQ 的高位
      • MQ 的低位用完之后直接丢弃
      • 此时，AC、MQ 中运算得到的位上的结果称作部分积
    • 数值位一共 n 位，则循环 n 次
      • 乘数的符号位不用参与运算。ACC+MQ 是一个整体，而 MQ 由取绝对值，所以最多只有 4 为有效，原本的符号位不会对结果造成影响。
      • 小数点隐含位置在 ACC 的第二位
    • 修改 ACC 的符号位：xs⊕ys=1
  • 之所以称为“一位乘法”是因为每次都使用 MQ 的最后一位进行乘积相加，还有更快的“二位乘法”但不做要求。
  • Tips：
    • 乘数的符号位不参与运算，可以省略
    • 原码一位乘可以只用单符号位，也可以用双符号位
    • 答题时最终结果最好写为原码机器数

补码的一位乘法（Booth算法）

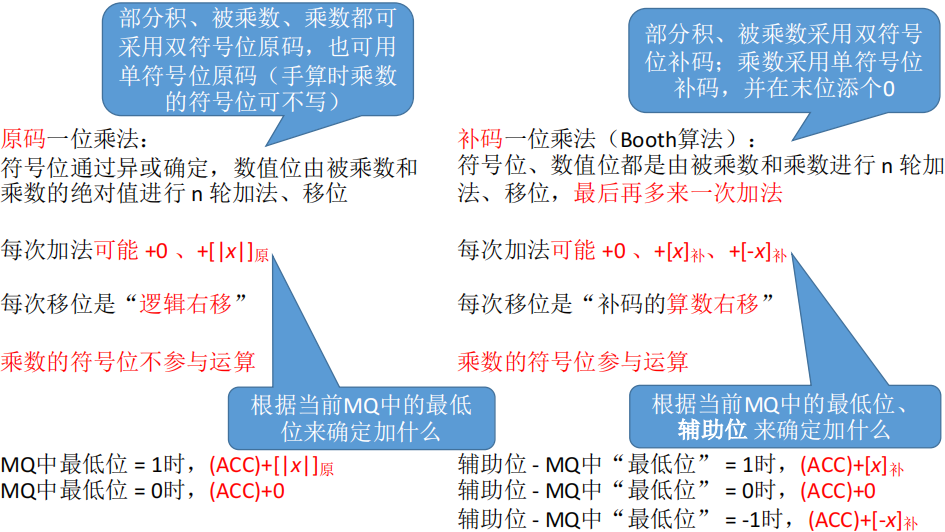
  • image-20211009134039359
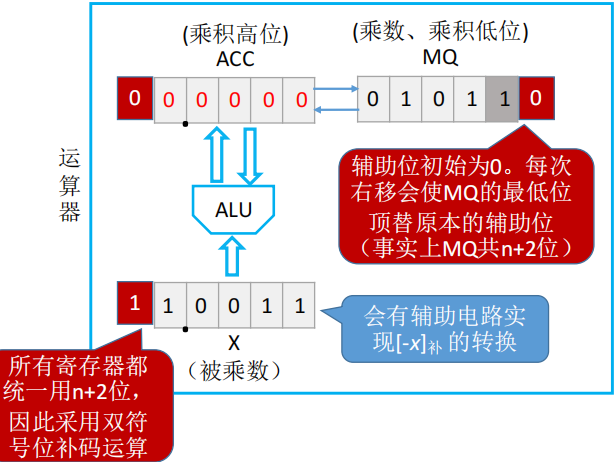
  • image-20211009143142389
  • 机器实现补码乘法时：
    • MQ 相比原码乘法需要在最低位后面加一位辅助位。同时 CPU 中寄存器大小应当一致，所以
      • ACC、X 使用双符号位，MQ 使用单符号位以及一位辅助位，部分积也是使用双符号位
    • 与原码乘法不同，每次加法是：ACC + [(辅助位-MQ最低位)x]补
    • 与原码乘法不同，每次移位是：补码的算数移位
      • 符号位不动，数值位右移，正数右移补0，负数右移补1（符号位是啥就补啥）
    • 加法与移位的循环分别是 n+1 和 n 次，即乘数的单符号位也会参与计算
    • 与原码乘法不同，最后的符号确定已在计算过程中完成，无需再次校验。

除法运算

除法运算的实现思想

  • 被除数、余数本质相同，是我们还需要去拼凑的数
  • 商是我们尽可能去接近需要拼凑的数但不能超过

原码的除法运算

恢复余数法
  • ACC 放被除数和余数，MQ 放商，X 放除数
  • 符号单独处理：符号位 = xs⊕ys
  • 数值位取绝对值进行除法计算
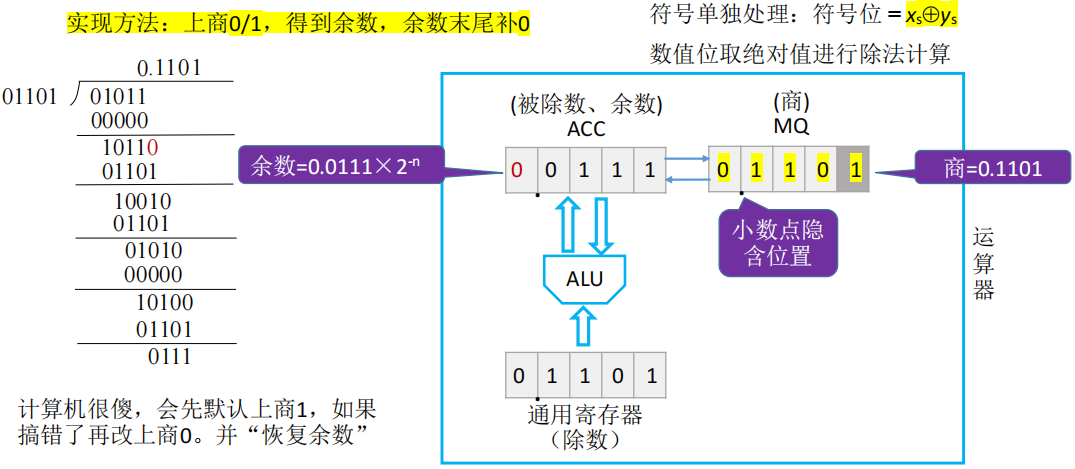
  • image-20211011153443169
  • 在机器实现除法中：
    • 在正式进行乘法之前，MQ 置零
    • 首先默认商/MQ最低位为 1，将除数的相反数的补码与被除数/余数（ ACC ）相加（将 ACC 减去除数）
      • (ACC)+ [−|y|]补 -> ACC
      • 若相减之后余数符号位为 1（小于 0），则表明商不应该为 1，而是 0
      • 则将 ACC 的值再次加上除数，恢复成原样
      • 并将商改成 0
      • 若最后一步余数是负数，则一样要进行上面的纠正
    • ACC、MQ 整体逻辑左移
      • MQ 低位补零
      • ACC 高位丢弃
    • 机器字长有 n+1 位，就要算 n+1 位的商，左移 n 次
    • 修改 MQ 的符号位：xs⊕ys=0
不恢复余数法（加减交替法）
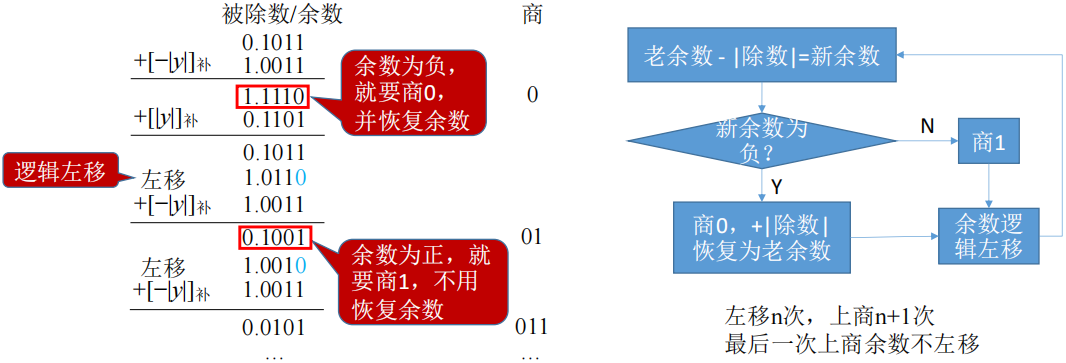
  • image-20211011155159488
  • image-20211011154706460
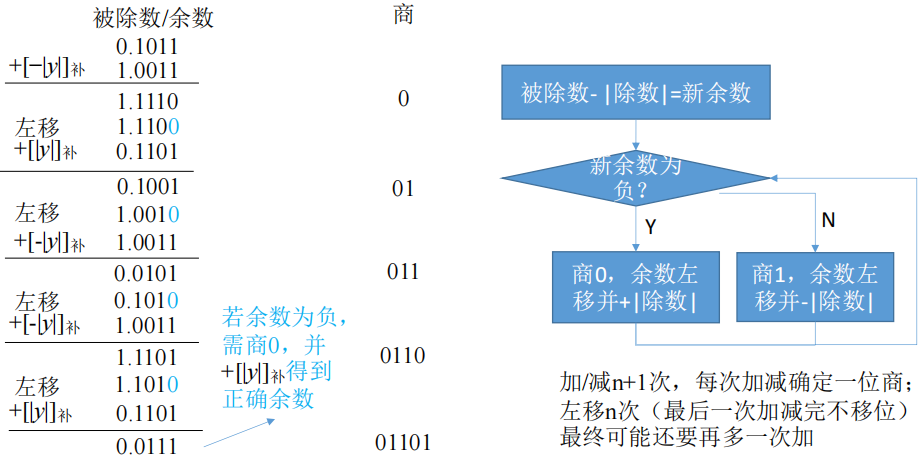
  • image-20211011155635905
  • 当余数（ACC）为负时，商 0
    • 恢复余数法：+|除数（X）|，再左移，再-|除数（X）|
    • 加减交替法：左移，再+|除数（X）|
  • 在加减交替法中
    • 余数（ACC）的正负性与商相同
    • 符号位同样需要额外判定
    • 若最后的余数（ACC）为负，需商0，并+[|y|]补得到正确余数

补码的除法运算（加减交替法）

  • 符号位参与运算
  • 被除数/余数、除数采用双符号位
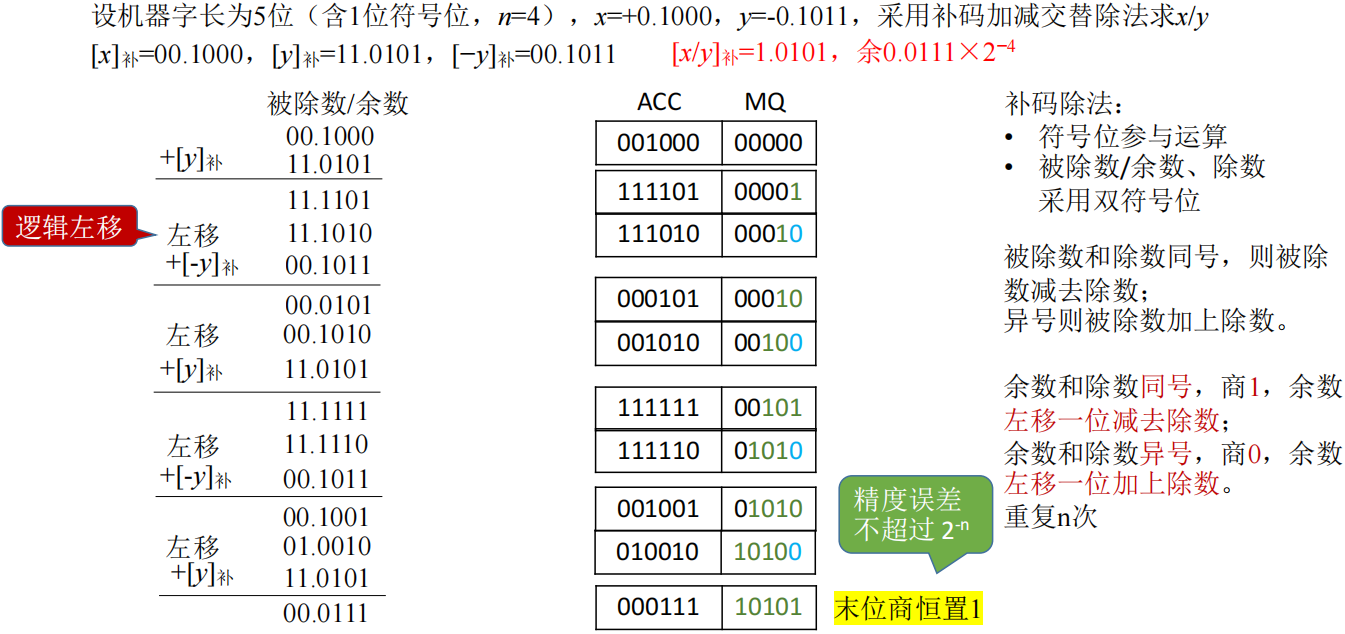
  • image-20211014133724204
  • 第一步，比较被除数（ACC）和除数（X）符号
    • 同号，则被除数-除数
    • 异号，则被除数+除数
  • 然后，比较余数（ACC）和除数（X）符号（每次循环保证两者相加符号不同，结果与被除）
    • 同号，商1，余数左移，减去除数
    • 异号，商0，余数左移，加上除数
  • 重复 n 次
  • MQ 的最后一位恒置 1（精度误差不超过 2^-n^）

除法运算总结

除法类型 符号位参与运算 加减次数 移位方向 移位次数 上商、加减原则 说明
原码加减交替法 否 N+1 或 N+2 左 N 余数的正负 若最终余数为负，则恢复余数
补码加减交替法 是 N+1 左 N 余数和除数是否同号 商末位恒置 1

强制类型转换

  • C 语言中定点整数（int、long、short）是用补码存储的。
  • image-20211015192650002

数据的存储和排列

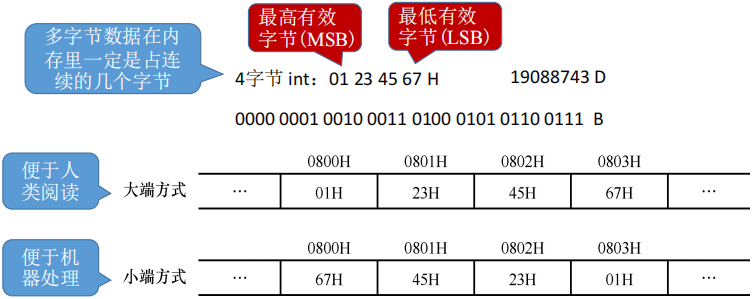
  • image-20211015195134394
  • 最高有效字节（MSB）最低有效字节（LSB）
  • image-20211015200927531
  • 现代计算机通常是按字节编址，即每个字节对应1个地址
    • 通常也支持按字、按半字、按字节寻址
  • 假设存储字长为32位，则1个字=32bit，半字=16bit
    • 要将按字寻址转成按字节寻址，则将值左移2位
  • 每次访存只能读/写1个字
  • c语言的数据类型长度
    • char：1字节
    • short：2字节
    • int：4字节
    • long：8字节
  • 使用边界对齐方式可以提高读取效率，而使用边界不对齐方式可以减少存储开销。

浮点数的表示与运算

浮点数的表示

浮点数的作用和基本原理

  • 针对问题：定点数可表示的数字范围有限，但我们不能无限制地增加数据的长度
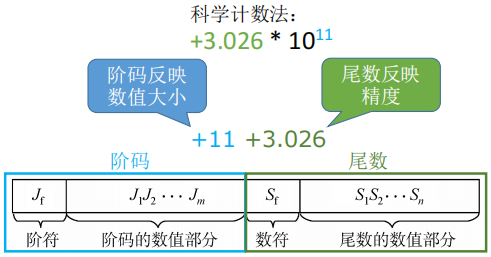
  • image-20211016153947660
  • 阶码：常用补码或移码表示的定点整数
  • 尾数：常用原码或补码表示的定点小数
  • 浮点数的真值：N=r^E^×M
    • 阶码的底 r，通常为 2
    • 阶码 E 反映浮点数的表示范围及小数点的实际位置
    • 尾数 M 的数值部分的位数 n 反映浮点数的精度
    • 尾数给出一个小数，阶码正负与数值指明了尾数左移/右移(小数点向后/向前移动)几位。

浮点数规格化

  • 规格化浮点数：规定尾数的最高数值位必须是一个有效值 。
  • 左规：当浮点数运算的结果为非规格化（尾数的最高数值位为 0）时，将尾数算数左移 1 位，阶码减 1。
    • image-20211016194214228
  • 右规：当浮点数运算的结果尾数出现溢出（双符号位为01或10）时，将尾数算数右移 1 位，阶码加 1。
    • 第一位符号位是正确的符号位
    • image-20211016194118837
  • 规格化浮点数的特点：
    • image-20211016204436786
    • 规格化的原码尾数，最高数值位一定是 1
    • 规格化的补码尾数，符号位与最高数值位一定相反

浮点数表示范围（大纲外）

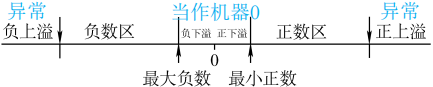
  • image-20211016204413711
  • 对于下溢，只需要当做0处理
  • 对于上溢，必须作为异常

浮点数标准IEEE75

  • 读音：I triple E——IEEE

  • 移码的定义：移码 = 真值 + 偏置值（偏置值并不固定）

    • 在之前所学的移码中：偏置值为 128D=1000 0000B，即 2^n-1^
    • 在 IEEE75 中，偏置值为 127D=0111 1111B，即 2^n-1^-1

  • image-20211018121445755

  • 阶码全1、全0时用作特殊用途。因此阶码的正常范围：**-126~127**

    • 规格化短浮点真值：(-1)^s^×1.M×2^E-127^
    • 规格化长浮点真值：(-1)^s^×1.M×2^E-1023^
    • 计算移码/阶码的真值时，不用在二进制上面计算，可以先把看见的移码当做无符号数计算值，然后减去偏置值127
类型 数符 阶码 尾数 总位数 偏置值（十六进制） 偏置值（十进制）
短浮点数(float) 1 8 23 32 7FH 127
长浮点数(double) 1 11 52 64 3FFH 1023
临时浮点数(long double) 1 15 64 80 3FFFH 16383

  • image-20211018115935229

  • IEEE 754 单精度浮点型能表示的最小绝对值、最大绝对值

    • 最小绝对值：尾数全为0，阶码真值最小-126，对应移码机器数 0000 0001。此时整体的真值为 (1.0)2×2^-126^
    • 最大绝对值：尾数全为1，阶码真值最大 127，对应移码机器数 1111 1110。此时整体的真值为 (1.111…11)2×2^127^
格式 格式化的最小绝对值 格式化的最大绝对值
单精度 E=1，M=0：1.0×2^1−127^=2^-126^ E=254，M=.11…1：1.11…1×2^254−127^=2^127^×(2−2^−23^)
双精度 E=1，M=0：1.0×2^1−1023^=2^-1022^ E=254，M=.11…1：1.11…1×2^2046−1023^=2^1023^×(2−2^−52^)
  • 只有 1≤E≤254时，真值 = (−1)^s^×1.M×2^E−127^
  • 当阶码E全为0
    • 尾数M不全为0时，表示非规格化小数 ±(0.xx…x)2×2^-126^
      • 隐含最高位变为 0
      • 阶码真值固定视为 -126
    • 尾数M全为0时，表示真值 ±0
  • 当阶码E全为1
    • 尾数M不全为0时，表示非数值 “NaN” (Not a Number)
      • 如：0/0、∞-∞ 等非法运算的结果就是 NaN
    • 尾数M全为0时，表示无穷大 ±∞

由浮点数确定真值（阶码不是全0、也不是全1）：

  1. 根据“某浮点数”确定数符、阶码、尾数的分布
  2. 确定尾数 1.M（注意补充最高的隐含位1）
  3. 确定阶码的真值 = 移码 - 偏置值 （可将移码看作无符号数，用无符号数的值减去偏置值）
  4. (−1)^s^×1.M×2^E−偏置值^

浮点数的运算

浮点数的加减运算

  • 浮点数加减运算步骤
    • 转换格式（真值D->机器数B；注意审题：用补/移码表示阶码和尾数）
    • 对阶（使两个数的阶码相等，小阶向大阶看齐，尾数毎右移一位，阶码加1）
    • 尾数加减
    • 规格化
    • 舍入（可以有不同的舍入规则）
      • 0舍1入：移去为0则舍，为1则入（可能会使尾数又溢出，此时需再做一次右规。）
      • 恒置1：无论移去0还是1，都使右移后的尾数末位置1（这种方法同样有使尾数变大和变小的两种可能。）
    • 判溢出（尾数溢出未必导致整体溢出，只有阶数溢出才是真正的溢出）
  • image-20211018135039513

强制类型转换

类型 16位机器 32位机器 64位机器
char 8 8 8
short 16 16 16
int 16 32 32
long 32 32 64
long long 64 64 64
float 16 32（23+1） 32
double 64 64（52+1） 64
  • 没有特殊说明，则默认 32 位机器
  • 无损转换：char -> int -> long -> double；float -> double。
    • 在 32 位中，这些转换过程没有损失
    • 在 64 位中，long -> double 会出现精度损失
  • 有损转换：int -> float；float -> int
    • 判断是否会有精度损失，要从有效数字方面考虑
    • int：表示整数，范围 -2^31^ ～ 2^31^-1 ，有效数字 32 位
    • float：表示整数及小数，范围 ±[2^-126^ ～ 2^127^×(2−2^−23^)]，有效数字 23+1=24 位
    • int -> float：可能损失精度（如 2^24^~2^31^-1 中无法被 float 表示的）
    • float -> int：可能溢出（范围过大）及损失精度（表示小数）

算术逻辑单元（ALU）

电路的基本原理、加法器设计

作用与原理

  • 机器字长是 CPU（ALU）一次能够处理的长度，一般等于寄存器的长度。因为输入输出数据存放的寄存器也要和 CPU 处理长度一致。
  • ALU 的功能。由控制单元 CU 发出的控制信号决定
    • 算术运算：加、减、乘、除等
    • 逻辑运算：与、或、非、异或等
    • 辅助功能：移位、求补等

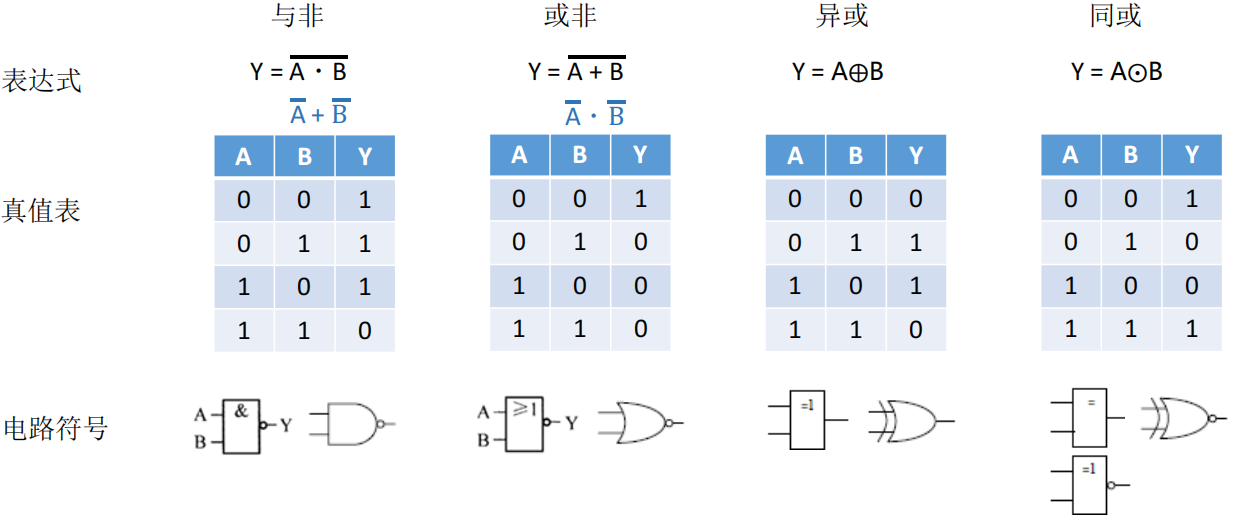
电路基础知识

image-20211018152119179

加法器的实现

一位全加器

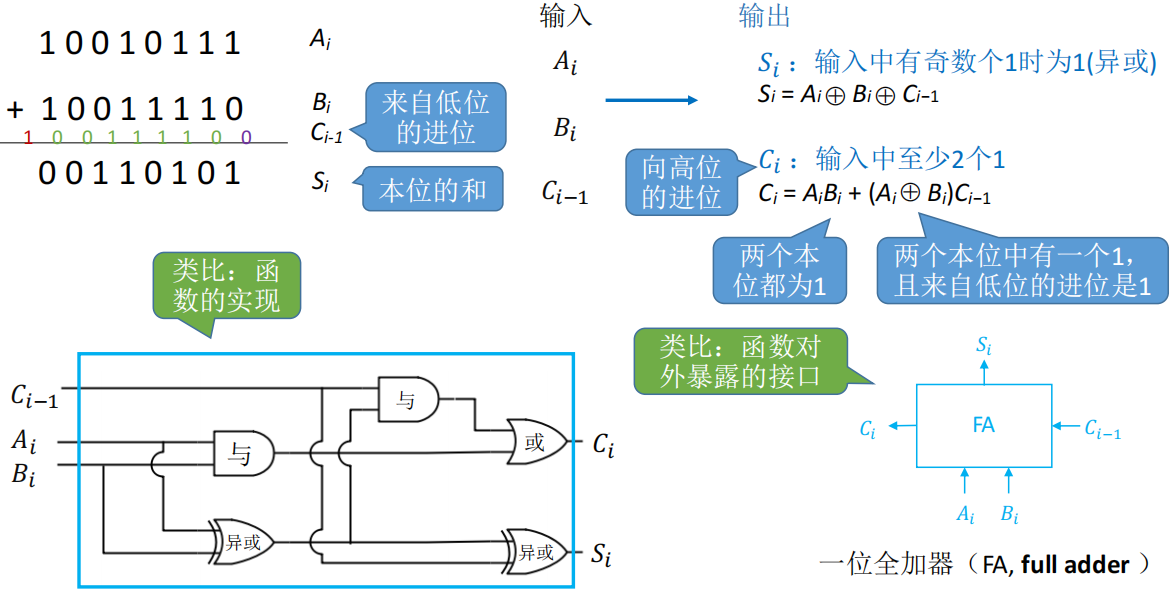image-20211018153352014、

串行加法器

image-20211018153857365

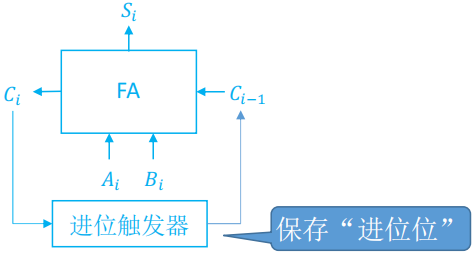
  • 串行加法器：只有一个全加器，数据逐位串行送入加法器中进行运算。
    • 进位触发器用来寄存进位信号，以便参与下一次运算。
  • 如果操作数长 n 位，加法就要分 n 次进行，每次产生一位和，并且串行逐位地送回寄存器。
并行加法器

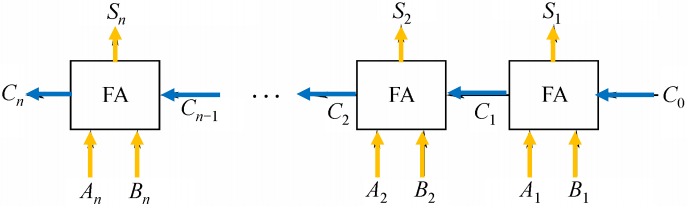
image-20211018153931233

  • 串行进位的并行加法器：把 n 个全加器串接起来，就可进行两个 n 位数的相加。
  • 串行进位又称为行波进位，每一级进位直接依赖于前一级的进位，即进位信号是逐级形成的。
  • 其性能很大程度依赖于 FA 产生进位和传递进位的速度

加法器、ALU的改进

  • 第 i 位向更高位的进位 Ci 可根据 被加数、加数的第 1~i 位、C0 即可确定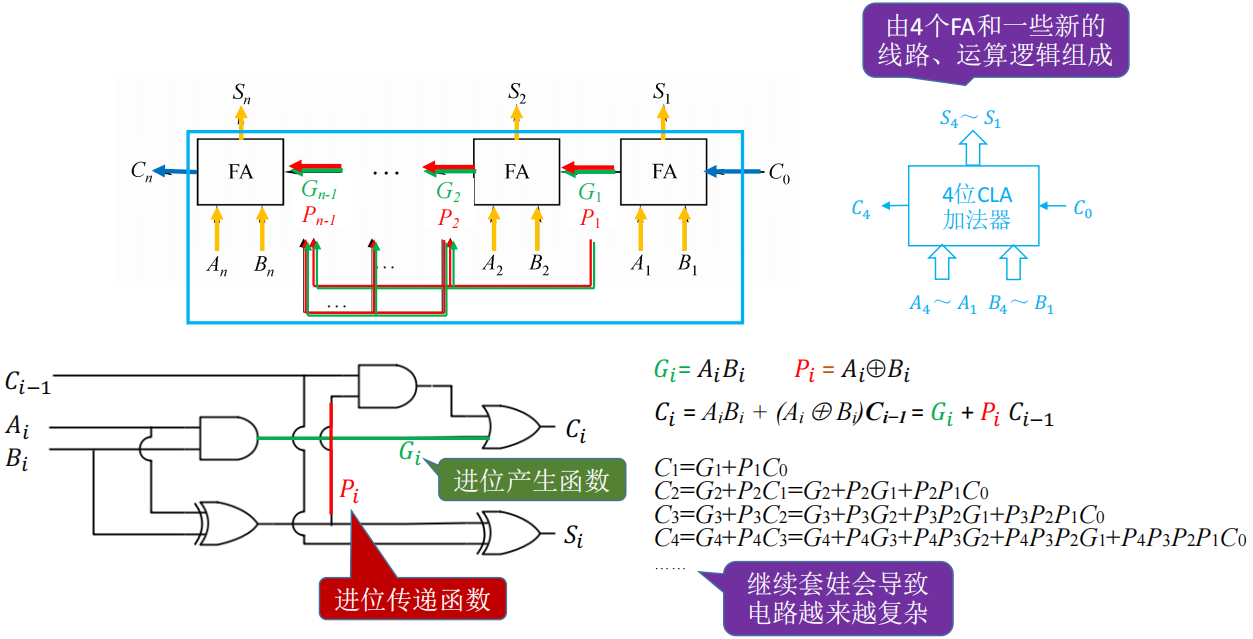
  • image-20211018171510387
  • 并行进位的并行加法器：各级进位信号同时形成，又称为先行进位、同时进位
  • 为了避免电路过于复杂，设计为 4 个 FA 为一组，组成一个 CLA
  • Gi：进位产生函数。（由本位确定的是否进位）
  • Pi：进位传递函数。（本位会控制/屏蔽前一位的进位信息）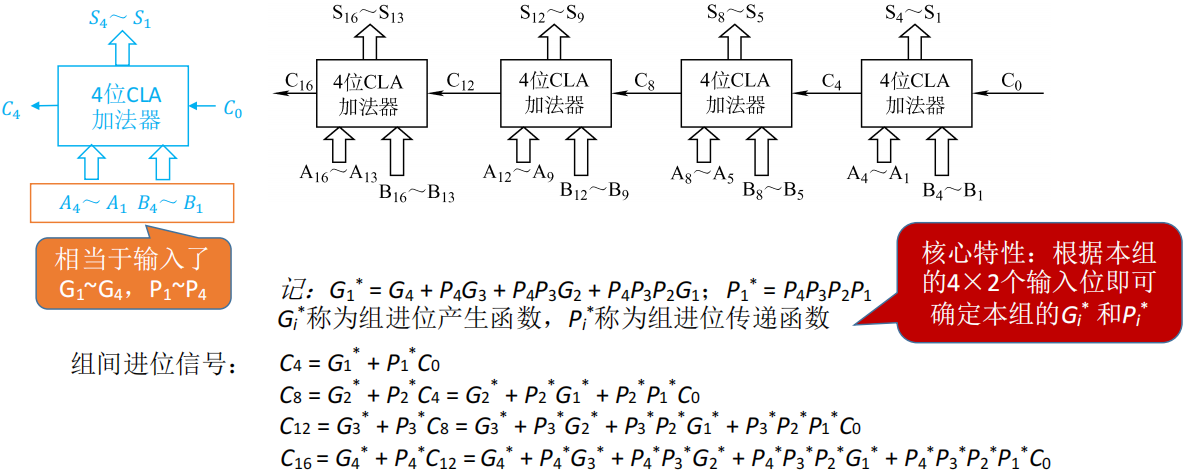
  • image-20211018172125934
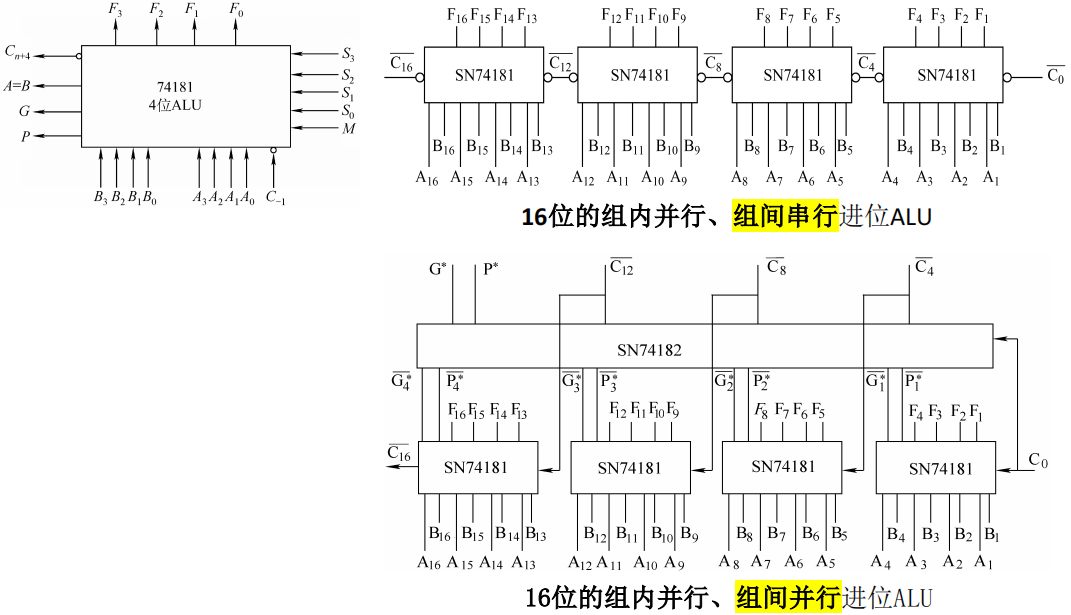
  • 完成组内并行之后，各组之间依然是串行的结构
    • 单级先行进位方式，又称为组内并行、组间串行进位方式。
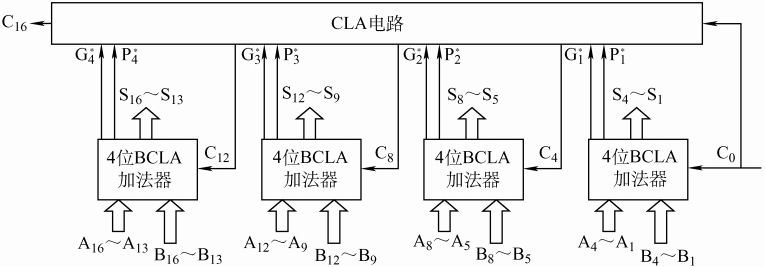
  • image-20211018172358547
  • 通过 CLA 电路，同时产生各组之间的进位信息
    • 多级先行进位方式，又称为组内并行、组间并行进位方式
  • image-20211018173324132

习题课

todo