OpenCV-Part4
OpenCV-Part4——图像处理(下)
[TOC]
直方图
定义
直方图,是在X轴上具有像素值(不总是从0到255的范围),在Y轴上具有图像中相应像素数的图。
直方图,可以用来总体了解图像的强度分布。
直方图只是理解图像的另一种方式。通过查看图像的直方图,可以直观地了解该图像的对比度,亮度,强度分布等。
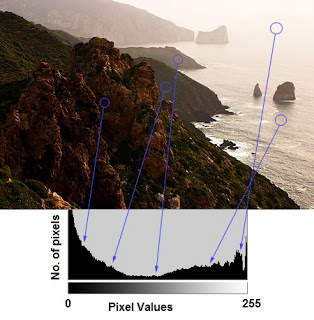
如图,此直方图是针对灰度图像而非彩色图像绘制的。其左侧区域显示图像中较暗像素的数量,而右侧区域则显示明亮像素的数量。
从该直方图中,可以看到暗区域多于亮区域,而中间灰度值的数量就非常少。
有关直方图的术语:
- BINS:像素值的区间段数。将整个直方图在 x 轴上分成 n 个子部分,每个子部分的值就是其中所有像素数的总和,每个子部分都称为一个 BIN 。当 x 轴采用 255 个值来展示直方图时,BINS=255。可用于对具体像素精度不在乎,而意图找固定区间段划分的像素总量的情况。在 OpenCV 中也称作 histSize 。
- DIMS:收集数据的参数量。当仅收集关于强度值的一件事的数据时,这里是1。
- RANGE:测量的强度值范围。通常为[0, 256],即所有强度值。
查找并绘制直方图
OpenCV计算直方图
cv2.calcHist(images,channels,mask,histSize,ranges,hist,accumulate):查找直方图。images:uint8或float32类型的源图像。需要由列表[img]包裹。channels:计算直方图的通道索引。对于灰度图像,则其值为[0]。对于彩色图像,可以传递[0]、[1]或[2]分别计算蓝色,绿色或红色通道的直方图。需要由列表[channels]包裹。mask:图像掩码。None:查找完整图像的直方图。否则为查找特定区域mask掩码的直方图。histSize:像素值的区间段数。需要放在方括号中。对于全尺寸,我们通过[256]。需要由列表[histSize]包裹。ranges:测量的强度值范围。通常为[0, 256]。
- Numpy 也有计算直方图的函数,但是
cv2.calcHist()比np.histogram()快大约40倍。因此,尽可能使用OpenCV函数。
1 | img = cv2.imread('home.jpg', 0) |
Matplotlib绘制直方图
matplotlib.pyplot.hist():Matplotlib自带直方图绘图功能,能够直接找到直方图并将其绘制。而无需使用cv2.calcHist()查找直方图。import numpy as np import cv2 from matplotlib import pyplot as plt image = cv2.imread('home.jpg') # numpy的ravel函数功能是将多维数组降为一维数组 plt.hist(image.ravel(), bins=256, range=[0, 256], histtype="step", color='black') # 对整图的,需要注意和灰度是有区别的! plt.hist(image[:, :, 0].ravel(), bins=256, range=[0, 256], histtype="step", color='blue') plt.hist(image[:, :, 1].ravel(), bins=256, range=[0, 256], histtype="step", color='green') plt.hist(image[:, :, 2].ravel(), bins=256, range=[0, 256], histtype="step", color='red') plt.show()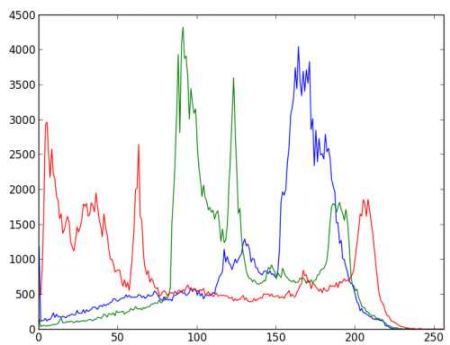1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
2. `cv2.calcHist()`+`plt.plot()`:先找到直方图数据,再使用matplotlib的法线图。分离了数据和画图,更符合程序解耦设计。
- ```python
import numpy as np
import cv2
from matplotlib import pyplot as plt
image = cv2.imread('home.jpg')
color = ["blue", "green", "red"]
ranges = [0, 256]
# 同时列出数据下标和数据
for i, color in enumerate(color):
hist = cv2.calcHist([image], channels=[i], mask=None, histSize=[256], ranges=ranges)
print(type(hist), hist.shape) # <class 'numpy.ndarray'> (256, 1)
plt.plot(hist, color=color)
plt.xlim(ranges)
plt.show()
直方图均衡化
定义
- 直方图均衡化,可以使限制在某一区间的色彩亮度均衡到整个色彩区间上,使像素在直方图上的分布更均匀。
- 直方图均衡化,是用来改善图像的全局亮度和对比度的。例如,在对人脸数据进行训练之前,对人脸图像进行直方图均衡化处理,使其具有相同的光照条件。

全局均衡化
cv2.equalizeHist():只能输入灰度图像,输出直方图均衡化后的图像。np.hstack((img1, img2)):横向拼接。
1 | equ = cv2.equalizeHist(img) |

自适应直方图均衡化(CLAHE)
- 当一张图同时拥有较多暗部和亮部时,全局均衡化极其容易丢失信息。
- 自适应直方图均衡,可以将图像分成称为 tiles 的小块(在 OpenCV 中,tileSize 默认为 8x8 )。并在每个较小的区域中,进行直方图均衡。
- 如果在 tiles 中有噪音,则应用了对比度限制:任何直方图 bin 超出指定的对比度限制(在OpenCV中默认为40),则在应用直方图均衡之前,将这些像素裁剪并均匀地分布到其他bin。
cv2.createCLAHE(clipLimit, tileGridSize):CLAHE 自适应直方图均衡化。clipLimit:颜色对比度的阈值。titleGridSize:进行像素均衡化的网格大小。
1 | cl1 = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8, 8)).apply(img) |

二维直方图
定义
- 上述都是在计算一维直方图,因为仅考虑一个特征,即像素的灰度强度值。
- 但是在二维直方图中,需要考虑两个特征:每个像素的
色相(Hue)和饱和度(Saturation)值。 - 二维直方图,通常用于查找颜色直方图。
查找并绘制直方图
OpenCV计算二维直方图
对于颜色直方图,我们需要将图像从BGR转换为HSV。对于一维直方图,我们从BGR转换为灰度
cv2.calcHist():对于二维直方图,使用相同的函数,但其参数将进行如下修改:channels=[0, 1]:因为需要同时处理H和S平面。histSize=[180, 256]:对于H平面为180,对于S平面为256。ranges=[0, 180, 0, 256]:色相值介于0和180之间,饱和度介于0和256之间。
1 | import cv2 |
Matplotlib绘制二维直方图
- matplotlib.pyplot.imshow():绘制2D直方图。
- 使用此功能时,插值法应采用最近邻以获得更好的结果。
1 | import cv2 |
下面是输入图像及其颜色直方图。X轴显示S值,Y轴显示色相。
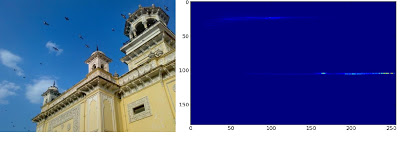
在该直方图中,可以在H = 100 和 S = 200 附近看到一些较高的值,对应于天空的蓝色。同样,在 H = 25 和 S = 100 附近可以看到另一个峰值,对应于宫殿的黄色。
YUV色彩空间对彩色图像做直方图均衡化
YUV色彩空间是把亮度(Luma)与色度(Chroma)分离。
- “Y”表示亮度,也就是灰度值。
- “U”表示蓝色通道与亮度的差值。
- “V”表示红色通道与亮度的差值。
对彩色图像进行直方图均衡化时,先将图像从RGB空间转到YUV空间,然后对亮度Y通道进行直方图均衡化得到通道Y”,然后将Y”UV通道进行合并。
1 | import cv2 |
直方图比较
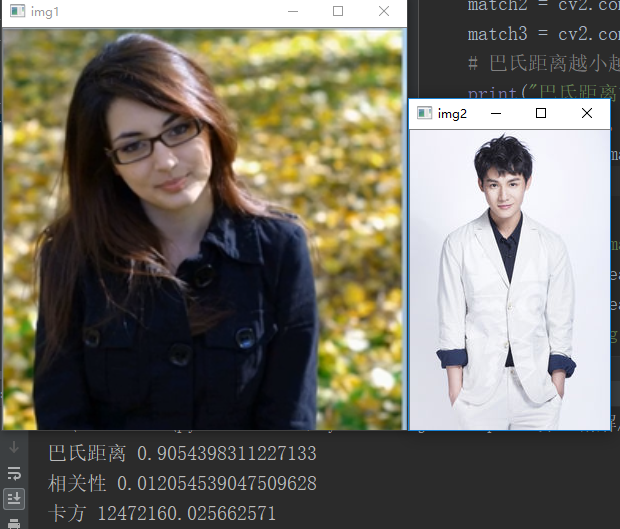
- 对输入的两张图像进行直方图均衡化后,可以对两个图像的直方图进行对比,从对比的结果得到一些的结论。
cv2.compareHist(H1, H2, method):对比两个图像的直方图。method有三中可用:cv2.HISTCMP_BHATTACHARYYA:巴氏距离,越小越相似。cv2.HISTCMP_CORREL:相关性,越大越相似。cv2.HISTCMP_CHISQR:卡方,越大越不相似。
1 | import cv2 |
直方图反投影
定义
- 直方图反投影,常用于图像分割或在图像中查找感兴趣的对象。本质是定位模板图像在输入图像的位置。
- 直方图反投影,一般使用的是颜色直方图,颜色直方图比灰度直方图更容易定义对象。
- 流程:1. 选定一个目标图像,这个图像应包含并尽可能填充我们的检测目标对象;2. 创建该图像的直方图;3. 将该直方图反投影到需要检测的测试图像上,计算出每个像素属于该目标的概率。
- 直方图反投影可以与 camshift 算法等配合使用。
- 我选择 U-Net。
OpenCV的反投影
cv2.calcBackProject(images, channels, hist, ranges, scale, dst):hist:目标进行归一化后的直方图。
1 | import numpy as np |
如下示例中,蓝色矩形的区域为目标对象,使用直方图反投影提取整个地面。

傅里叶变换
定义
傅立叶变换,可以用于分析各种滤波器的频率特性。
对于正弦信号:如果幅度在短时间内变化快,则为高频信号;如果变化慢,则为低频信号。
可以将相同的想法扩展到图像:图像中的振幅在边缘点或噪声急剧变化,边缘和噪声就是图像中的高频内容;如果图像中幅度没有太大变化,则就是低频分量。
傅里叶变换,可以将一幅图片分解为正弦和余弦两个分量,即可以将一幅图像从其空间域(spatial domain)转换为频域(frequency domain)。
详细讲解傅里叶的文章:
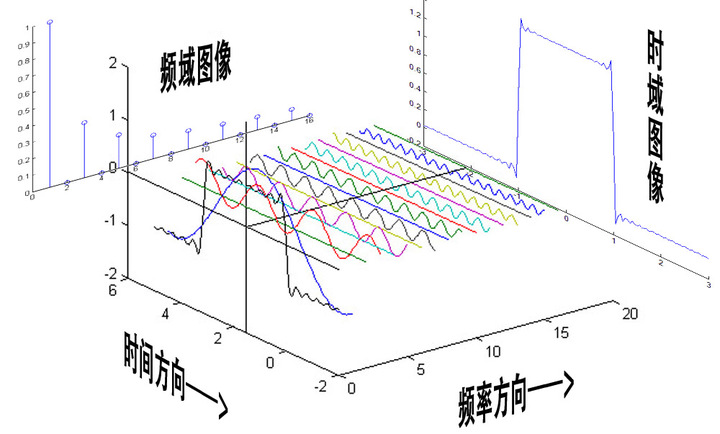
正弦波就是一个圆周运动在一条直线上的投影。所以频域的基本单元也可以理解为一个始终在旋转的圆:
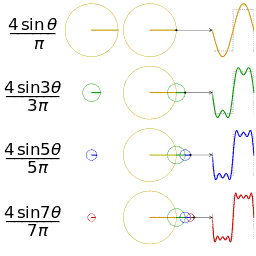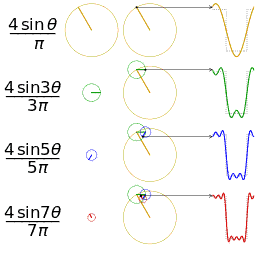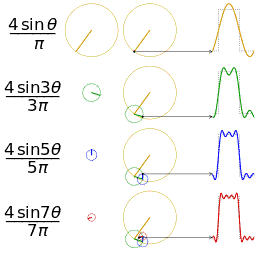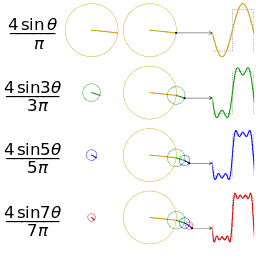
时域与频域之间的联系:
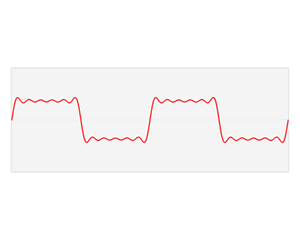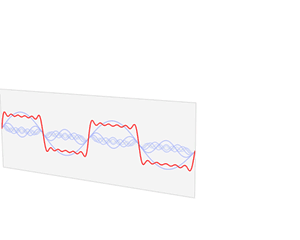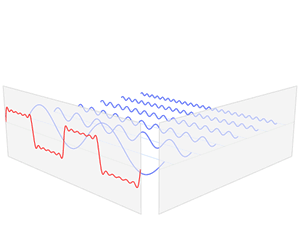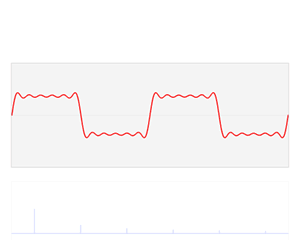
效果
灰度图 与 傅里叶变换:
可以看到白色区域大多在中心,显示低频率的内容比较多。

傅里叶变换删去低频内容:
删除图像中的低频内容,即将HPF应用于图像,本质是提取边缘。
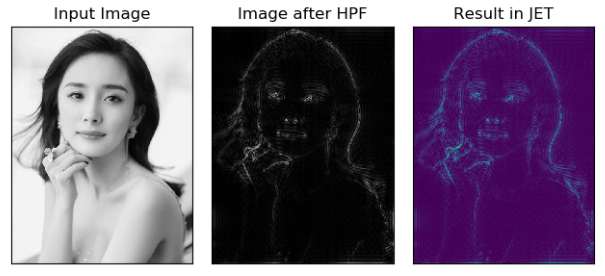
傅里叶变换删去高频内容:
删除图像中的高频内容,即将LPF应用于图像,本质是模糊图像。

各滤波器是 HPF(High Pass Filter)还是 LPF(Low Pass Filter):
白点在中间的就是 LPF ,白点在四周的就是 HPF。

实现
- 对于图像,可以使用2D离散傅里叶变换(DFT, 2D Discrete Fourier Transform)查找频域。同时,可以使用快速傅立叶变换(FFT, Fast Fourier Transform)的快速算法用于DFT的计算。
- OpenCV使用
cv2.dft()、cv2.idft()实现傅里叶变换,效率更高。 - Numpy使用
np.ifft2()、np.fft.ifftshift()实现傅里叶变换,使用更友好。 - DFT的性能优化:在一定的阵列尺寸下,DFT计算的性能较好。当数组大小为2的幂时,速度最快。大小为2、3和5的乘积的数组也可以非常有效地处理。
为达到最佳性能,可以通过OpenCV提供的函数cv2.getOptimalDFTSize()寻找最佳尺寸。
然后将图像填充成最佳性能大小的阵列:1. 对于OpenCV,必须手动填充零;2. 对于Numpy,可以指定FFT计算的新大小,自动填充零。 - 通过使用最优阵列,大概能提升4倍的效率。而OpenCV本身也比Numpy效率快近3倍。
Numpy中的傅里叶变换
1 | import cv2 |
OpenCV中的傅里叶变换
1 | import cv2 |
HPF or LPF
1 | import cv2 |
模板匹配
- 模板匹配,在较大图像中查找模板图像位置的方法。
- 我选择深度学习。
OpenCV中的模板匹配
1 | import cv2 |
多对象模板匹配
1 | import cv2 |