浙江大学机器学习课程Part6——传统的机器学习

[TOC]

特征选择与特征提取

特征选择与特征提取(Feature Selection and Extraction)

特征选择是一个”物理”过程，不会产生新特征；特征提取是一个”化学”过程，会产生新特征。

  1. 特征提取：主成分分析(Principle Component Analysis)
  2. 特征选择：自适应提升(AdaBoost)

主成分分析

主成分分析与神经网络

多层的神经网络，其本质也是一个特征提取器。但是，主成分分析主要目标是减少计算量。

主成分分析：构造一个A，b使：Y(M*1) = A(M*N) * X(N*1) + b(M*1)

主成分分析可以看成是一个一层的，有m个神经元的神经网络。

主成分分析的过程

主成分分析：寻找方差最大的方向，并在该方向投影。在降维的同时保存最大的区分度。

这里方差最大方向指的是投影之后方差和最大，因为如果投影之后点都汇集在一起的话，那么可以近似成一个点，就区分不出来了。

主成分分析详细推导P38

  1. 最大化寻找的特征方向上的方差和。

    max： a1∑a1^T^=λ；s.t.：a1*a1^T^=||a1||^2^=1 (ai是A的行向量)

  2. 寻找下方差和最大化的特征方向，并且需要与刚才的方向正交。

    max： a2∑a2^T^=λ；s.t.：a2*a2^T^=||a2||^2^=1、a1*a2^T^=a2*a1^T^=0

  3. a2是∑的特征向量，λ是∑的第二大特征值

  4. loop

PCA算法全程

  1. 求 ∑=∑i=1^i^(Xi-E(x))^T^

  2. 求∑的特征值并从大到小排序[λ1, λ1, λ2,…, λM, λM+1,… ]

    对应特征向量[a1^T^, a2^T^, …, aM^T^, aM+1^T^, …]

  3. 归一化所有ai，使aiai^T^=1

  4. A=[[–a1–],[–a2–],…,[–am–]]

  5. Yi=A(Xi-E(X))

其他算法

奇异值分解SVD(Singular Value Decomposation)快速求出特征值来完成PCA算法。

总结

在特征数比较多，样本数又比较少的情况下，采用PCA，效果不会差。

自适应提升(AdaBoost)

特征选择

从N个特征中选择M个使识别率更高。

（启发式方法，如模拟退火、基因算法）①递增法②递减法。不常用，因为神经网络已经做了这些事情，相关性不高的连线之间w会变得很小。

自适应提升

针对大规模冗余的特征样本时，是一个非常好的算法。

详细推导P39

  1. 初始化采样权值
  2. 用Dm采样N个样本（错的样本出现更多，对的样本出现更少），获得弱分类器
  3. 计算加权错误率
  4. 更新权值分布
  5. -> 2. loop
  6. 最终识别器

定理：随着M增加，AdaBoost最终分类器在训练集上错误率越来越小。

AdaBoost过拟合速度不会上升太快。

概率分类法==重点复习==

一定要特别注意先验概率！！！

朴素贝叶斯

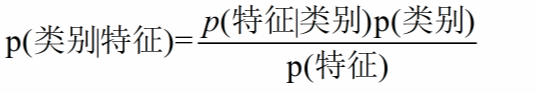
image-20210213210453656

限制条件：

  1. 每个维度都是离散的
  2. 每个维度互相独立

对于每个P(特征|类别)有：
$$
P(w|C_j)={count(w,C_j)+1\over{\sum\limits_{w∈V}cout(w,C_j)+|v|}}
$$
其中，Cj指某个类别j，V指特征集合，|v|指特征数。

高斯概率密度函数

正态分布（Normal distribution）又名高斯分布（Gaussian distribution）。

多维高斯分布：

$$
P(X|C)= {1\over{\sqrt[]{(1π)^d|∑|}}}exp[-{1\over2}(x-μ)^T∑^{-1}(x-μ)]
$$

已知{Xi}i={1-N} ，求待求参数：∑(d×d矩阵)、μ(d×1向量)

构造目标函数（极大似然法Maximum Likedihood）
$$
E(μ,∑)=\sum\limits_{i=1}^NlnP(X_i|C)
$$
假设：①所有{Xi}i={1-N}独立同分布 undependent and identical distribution ( i.i.d. )；②设定μ1、∑1使出现{Xi}i={1-N}概率最大。

先是概率累乘作为似然函数，取对数方便运算，连乘就变成求和了

详细推导p43

EM算法(Expectation-Maximization)

混合高斯模型(Gaussian Mixture Model)

叠加多个高斯分布拟合整个复杂的分布。

这是一个非凸问题，只能求局部极值，不能求全局极值。

求局部极值的一种方法，而且只对某一类局部极值问题可解。

优点：①不需要调任何参数，必定收敛②编程简单③理论优美

步骤：

  1. 随机化，先假设类别
  2. E-step 计算第n个样本在k个高斯的概率
  3. M-step 更新所有N个样本中有多少个属于第k个高斯
  4. ->2 loop

详细推导p45

EM算法收敛性推导

k-均值聚类(K-means Clustering)

  1. 随机化μ1、…、μk
  2. E-step 离哪个类近，重新归属于哪一类
  3. M-step n个样本中有多少个属于第k类，重新分配第k类的均值μk
  4. ->2 loop

GMM在说话人识别中的应用

  1. 去除静音(将不说话的低能量片段去除，但保留同为低能量的辅音(使用过零率判别))
  2. 提取的特征：MEL倒谱系数 （Mel-frequency Cepstrum Coefficients, MFCC）

缺点：对噪声要求严苛，因为加了噪声就相当于改变分布。