浙江大学机器学习课程Part5——强化学习

[TOC]

增强学习与监督学习的区别

  1. 训练数据中没有标签，只有奖励函数（Reward Function）。
  2. 训练数据不是现成给定，而是由行为（Action）获得。
  3. 现在的行为（Action）不仅影响后续训练数据的获得，也影响奖励函数（Reward Function）的取值。
  4. 训练的目的是构建一个“状态->行为”*(内部状态和外部状态，外部状态不由我们的行为控制)*的函数，其中状态（State）描述了目前内部和外部的环境，在此情况下，要使一个智能体（Agent）在某个特定的状态下，通过这个函数，决定此时应该采取的行为。希望采取这些行为后，最终获得最大化的奖励函数值。

定义

  1. Rt：t时刻的奖励函数
  2. St：t时刻的状态
  3. At：t时刻的行为

假设

  1. 马尔科夫假设：P[St+1|St]=P[St+1|S1,…,St]

  2. 下一个时刻的状态只与这一时刻的状态以及这一时刻的行为有关：

    PSS’^a^=P[St+1=s’|St=s, At=a]

  3. 下一时刻的奖励函数值值域这一时刻的状态以及这一时刻的行为有关：

    PS^a^=E[Rt+1|St=s, At=a]

Markov decision Process (MDP)

  1. 在t=0时候，环境给出一个初始状态 s ~ p(s0)
  2. 循环：
     -- 智能体选择行为：a~t~
 -- 环境采样奖励函数：r~t~ ~ R( . |s~t~, a~t~)
 -- 环境产生下一个状态：s~t+1~ ~ R( . |s~t~, a~t~)
 -- 智能体获得奖励函数 r~t~ 和下一个状态 s~t+1~
  3. 我们需要学习一个策略（Policy）π^*^(st,at)=P(at|st) , 这是一个从状态到行为的映射函数，使得最大化累积的奖励。

Q-Learning

数学推导

  1. 增强学习中已经知道的的函数是：PS^a^=E[Rt+1|St=s, At=a]
  2. 需要学习的函数是：PSS’^a^=P[St+1=s’|St=s, At=a]
  3. 根据一个决策机制（Policy），我们可以获得一条路径：s0 -> a0 -> r0 -> s1 -> a1 -> r1 …
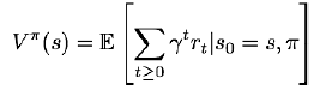
  4. 定义1：估值函数（Value Function）是衡量某个状态最终能获得多少累积奖励的函数：image-20210210225702878
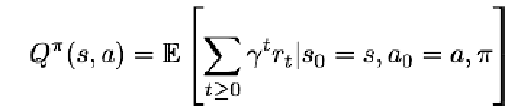
  5. 定义2：Q函数是衡量某个状态下采取某个行为后，最终能获得多少累积奖励的函数：image-20210210225720116
  6. 在s状态下做出行为a的概率，和这种情况下的奖励，得到估值 V^π^(s)=∑a∈AP(a|s)Q^π^(s,a)

劣势

  1. 对于状态数和行为数很多时，使Q函数非常复杂，难以收敛。例如：①对一个ATARI游戏，状态数是相邻几帧所有像素的取值组合，这是一个天文数字；②图像方面的应用，状态数是(像素值取值范围数)^(像素个数)
  2. 很多程序，如下棋程序等，REWARD是最后获得（输或赢），不需要对每一个中间步骤都计算REWARD。

总结

  1. 目前强化学习的发展状况：在一些特定的任务上达到人的水平或胜过人，但在一些相对复杂的任务上，例如自动驾驶等，和人存在差距。

  2. 和真人的差距，可能不完全归咎于算法。传感器、机械的物理限制等，也是决定性因素。

  3. 机器和人的另一差距是：人有一些基本的概念，依据这些概念，人能只需要很少的训练就能学会很多，但机器只有通过大规模数据，才能学会。

  4. 但是，机器速度快，机器永不疲倦，只要有源源不断的数据，在特定的任务上，机器做得比人好，是可以期待的。

Alpha Go

围棋有必胜策略

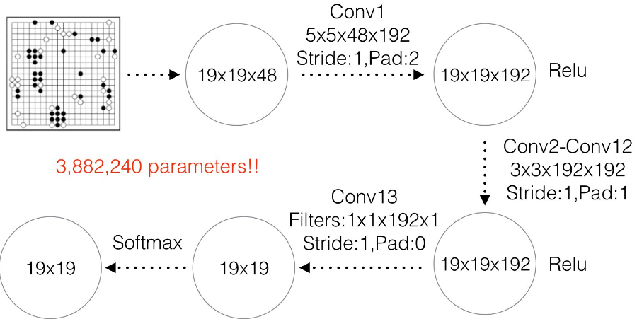
image-20210210235412124

Alpha Go 开源地址

每隔一定的轮次，训练过后的网络将和训练之前的网络对抗，已获得更多的样本数据继续训练。

另外有一个更加简单的深度策略网络(Rollout Policy Network)，牺牲准确率来换取速度，在对局后期通过不断演算，将赢的落子概率增加，输的概率减少。

蒙特卡洛树搜索 （Monte Carlo Tree Search）：多次模拟未来棋局，然后选择在模拟中选择次数最多的走法。

同时要采用多样化的步骤来增加随机性。

参考资料

  1. Reinforcement Learning an introduction. R. S. Sutton and A. G. Barto, 2005

  2. UCL Course on RL

  3. 例程程序

    http://karpathy.github.io/2016/05/31/rl/?_utm_source=1-2-2
    https://gym.openai.com/https://github.com/openai/gym