浙江大学机器学习课程Part3——人工神经网络

[TOC]

神经网络的生物及数学模型

  1. 硬件算力的提升
  2. 数据样本的增加
  3. 但是，其最基本的神经元模型至今没有重大改变

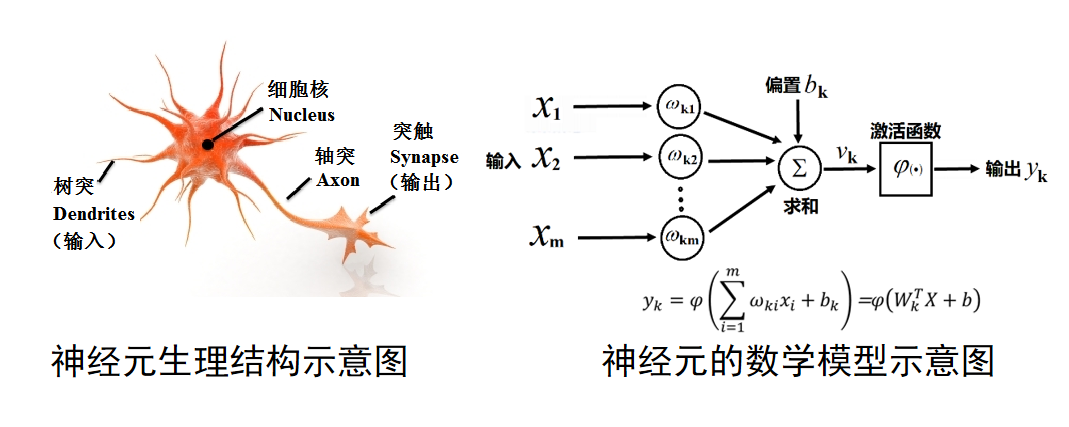
image-20210209144613134

感知器算法(Perceptron Algorithm)

image-20210209144950398

  • 效果比SVM差得多，但是是机器学习最早提出的算法。
  • 感知器每次只取单个样本，SVM从全局样本考虑。

收敛性证明看p20

多层神经网络(Multi-Layer Neural Networks)

线性不可分的数据集困扰了早期神经网络算法长达十年之久。

因此，我们需要用非线性的函数集合来分开非线性可分的数据集。

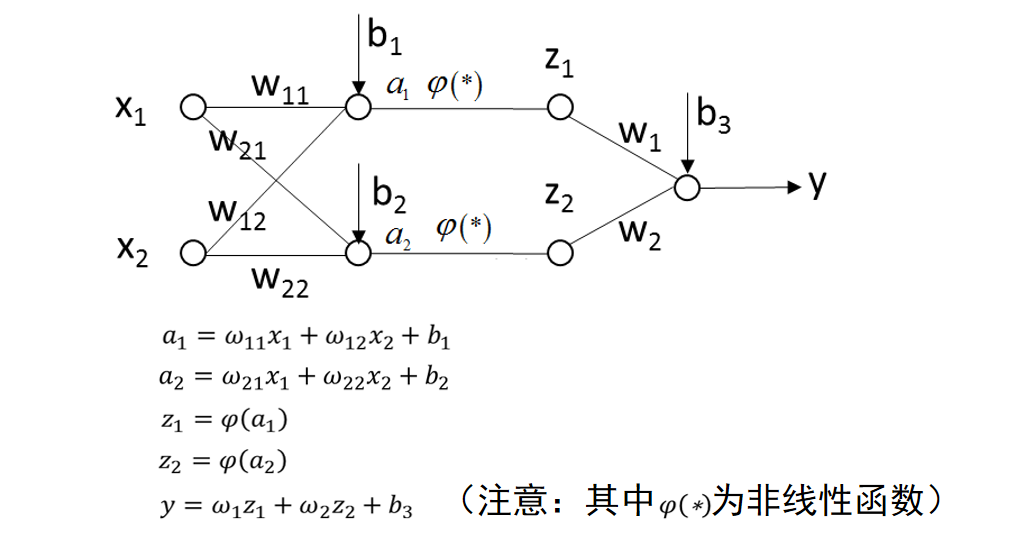
image-20210209160042159

二层神经网络模型举例。

三层神经网络模拟任意决策面

我个人认为：过了第一层，数据样本基本不会保持原貌，但是保留了特征，或者说特点。

在老师画的示例中，实际的数学意义为：①第一层是：坐标(x,y)进入多个函数输入相对位置，进入激活函数输出0-1；②第二层：根据上一层判断的0-1，进入函数判断是否为某一块图形内部，返回0-1；③第三层：根据上一层返回的是否在某图形内部的0-1，进入函数判断该图形是否为class1，通过或关系，输出最终结果0-1.

详情见p23

后向传播算法(Back Propagation)

在对于某种问题，我们究竟应该选择哪一种参数组合，如何搭建完美的网络结构。这依然是一个至今为止不完备的，对于一种问题，最好的方法还是不断试验。

主要思想就是梯度向下法(Gradient Descent Method)来求局部极值。

常用的激活函数：sigmoid、tanh、ReLu(Rectified Linear Units)、LeakReLu

==BP推导P24==

参数设置

随机梯度下降

  1. 不用每输入一个样本就去变换参数，而是输入一批样本（叫做一个BATCH或MINI-BATCH），求出这些样本的梯度平均值后，根据这个平均值改变参数。
  2. 在神经网络训练中，BATCH的样本数大致设置为50-200不等。

激活函数

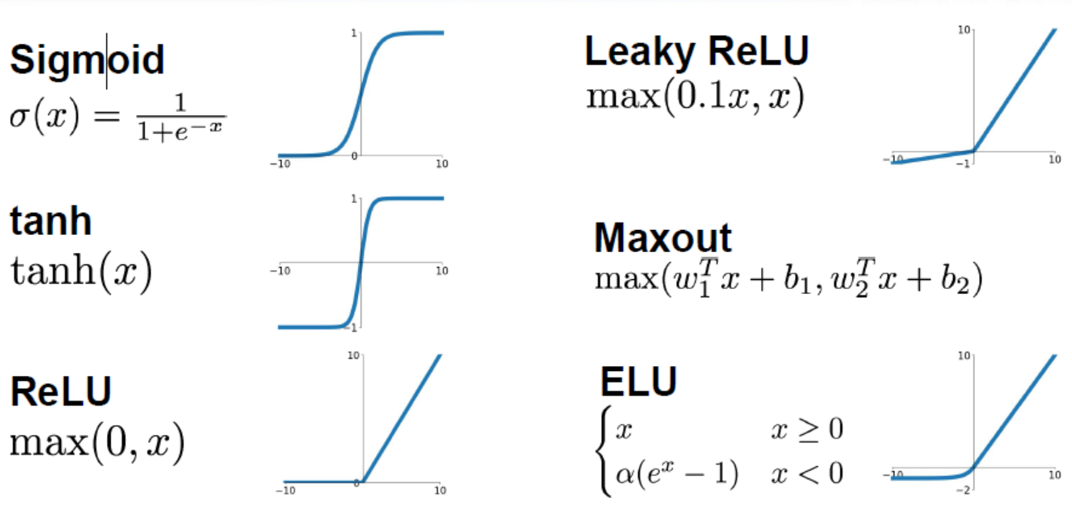
image-20210210140226760

梯度消失与归一化

  1. 当样本都非常大或者非常小，在sigmoid函数中就可以发现，他们的梯度将会非常小，这样意味着他们更加符合我们想要得到的预测结果，即二分类。但是这并不是我们在训练过程中想要的，因为梯度太小而导致参数无法更新以进行训练。
  2. 防止梯度消失，那么就需要使样本更加靠近在0附近，更加具有像线性模型一样的特性。因此我们经常对初始数据以及在训练过程中进行归一化Batch Normalization。

目标函数选择

  1. SOFTMAX函数

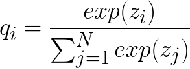    image-20210210131234229 处理多分类

  2. 交叉熵(Cross Entropy)

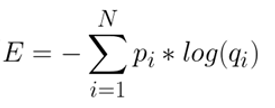    image-20210210131306125 处理二分类

参数更新策略

优化器不一定是MSE，因为MSE的更新通常容易出现z字路径，一般可以选择使用其他更加平滑的优化器，比如AdaGrad、RMSProp。