浙江大学机器学习课程Part2

浙江大学机器学习课程Part2——支持向量机

[TOC]

Support Vector Machine

支持向量机

对样本数较少的时候，都会得到一个比较好的结果。

如何在两种训练集上画一条直线来分类：

1. 线性可分(Linear Separable)训练样本集
2. 非线性可分(Non-Linear Separable)样本集

将线(在多维特征下是超平面Hyperplane)向两边移动直到擦到样本点，其中间隔(Margin)最大，且线在d/2处。

数学描述

1. 将平行线擦到的向量称作支持向量(Support Vector)
2. 训练数据及标签：(Xn, Yn)…… X为特征向量，Y为标签。Y取+1或-1来表示，方便推导。
3. 线性模型：(W, b) 超平面：Wt * X + b = 0

机器学习过程

1. 用复杂的函数来限定模型框架
2. 留出待定参数
3. 用训练样本来确定参数取值

线性可分的定义和条件

{(Xi, Yi)}i = 1N, 存在(W, b), 则对任意 i = 1N. 有：

①若Yi = +1, 则 Wt * X + b > 0

②若Yi = -1, 则 Wt * X + b < 0

为什么要取Y=±1？因为可以得到①②等价于 Yi ( Wt * X + b ) > 0

优化问题(优化目标函数和限制条件)

两个要点

1. 点最小化(Minimize / min): 1 / 2 * ||W||² 。这里1/2只是为了求导方便
2. 限制条件(Subject to / s.t.): Yi ( W^T^ * X + b ) ≥ 1, (i=1~N)

两个事实

事实1：W^T^ * X + b = 0 与 a * W^T^ * X + a * b = 0, (a∈R+) 是同一个平面。

​ 即: 若 (W, b) 满足 W^T^ * X + b = 0 , 则 (a * W, a * b) 也满足 W^T^ * X + b = 0

事实2：向量到超平面(点到平面)的距离公式。d = | Wt * X0 + b | / || W || *1.这里的X0代表的是包含多个维度的坐标[x,y,z…]，而Y0是分类标签，不能与坐标混为一谈；2.WtX0结果是一个数而不是矩阵向量**

​ 其中，模 || W || = √(W1²+W2²…+Wn²)

推导

1. 用a去缩放超平面参数：(W, b) <=> ( a * W, a * b )。根据事实1，这两组不同的参数代表的是同一个平面。
2. 最终使在支持向量上：| W^T^ * X0 + b | = 1。这里的W和b都是经过系数a缩放过后的，目的是为了凑出1(当然你可以凑出任意常数)，而a具体是多少，我们不需要关注。需要注意的是，这里只是带入支持向量的值，并不是指支持向量的那个点在超平面上，否则值为0。
3. 由推导2和事实2可得：d = | W^T^ * X0 + b | / || W || = 1 / || W ||。可得要点1：最小化 ||W|| 即最大化 d 。
4. 其他不是支持向量的点到超平面的距离，则大于 1 / || W || 。可得 | W^T^ * X0 + b | > 1 。可得要点2：限制条件 Yi * ( W^T^ * X + b ) ≥ 1

举例：原来平面是 W^T^ * X + b = 0 , 假设带入X0后的值 | W^T^ * X0 + b | = M , 现在把超平面缩放为 a * W^T^ * X + a * b = 0 , 其中a是1/M, 那么把X0带入则 | a * W^T^ * X0 + a * b | = M/M = 1。与此同时，计算d的时候，因为分子分母同乘a=1/M，a不需要求出，所以我们不需要关心a的取值，只是为了凑一个 | W^T^ * X0 + b | = 1 ，当然你可以凑出任意常数。

二次优化问题(Quadratic Programming)

二次优化问题属于凸优化问题

1. 目标函数(Obejective Function)是二次项
2. 限制条件是一次项

要么无解，要么只有唯一极值。即局部极值就是全局极值。

SVM处理非线性

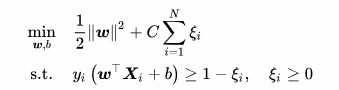
处理这种问题的一种方案就是加上正则项(Regulation Term)（结构损失函数），在解集合中挑选出一组参数（解），使经验损失和结构损失都较低。

c是正则化的强度，是事先设定好的超参数。

ζ是松弛变量(Slack Variable)。

放到场景中就是，样本数小于参数量，在只优化经验误差函数的时候很容易发生过拟合。这个公式依然可以适用于处理线性Linear SVM。

低维到高维映射

在低维空间中，一些线性不可分的数据集，在高维空间中，更有可能被分开。因此可以把Xi通过函数φ(x)变换映射到高维空间，通过泛函分析满足某种条件，把核函数W*φ(x)拆成两个高维向量的内积。

核函数

我们可以不在意无限维映射φ(x)的显示表达，我们只要知道一个核函数(kernel Function)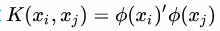，，则优化问题仍然可解。

线性内核相当于没有用核。多项式核的待定系数d取越大，则越复杂。高斯核是无限维度，分类效果最高，待定系数为σ。Tanh核的待定参数是β和b。这些待定参数的选取只能不停地试。

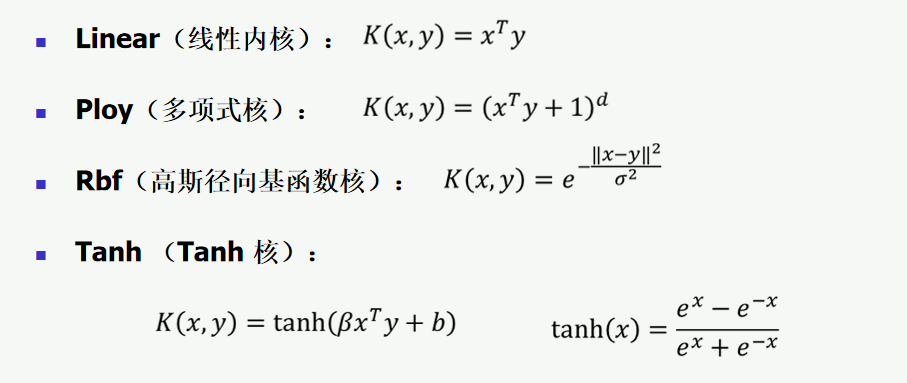
充要条件

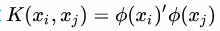能够成立的充要条件：(Mercer’s Theorem)

1. K(X1, X2) = K(X2, X1) (交换性)
2. 对任意 常数Ci, 向量Xi (i=1N)，有 ∑(i=1N) ∑(j=1N) Ci~ * Cj * K(Xi, Xj) ≥ 0 (半正定性)

原问题和对偶问题==(重点复习)==

优化理论

优化理论(运筹学)是工程里最本质的问题

推荐书籍

1. Convex optimization - Stephen Boyd - b站吴立德
2. Nonlinear Programming

原问题(Prime Problem)

min: f(w)

s.t. : gi(w)≤0 (i=1K) , hi(w)=0 (i=1M)

对偶问题(Dual Problem)

1. 定义：

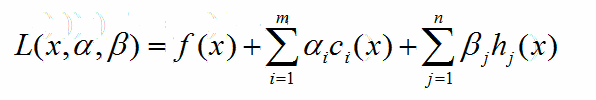
   x是前面的w，α是一个K维的向量，β是一个M维的向量。

   拉格朗日对偶问题是运筹学基础知识。*(KKT条件求解、拉格朗日传乘数法、弱对偶性定理)*

2. 对偶问题定义：

   max: 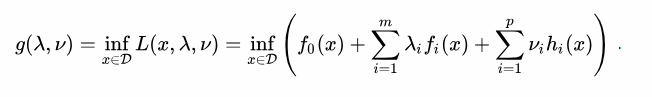(inf:求最小值)

   s.t. : λi ≥ 0 (i=1~K)

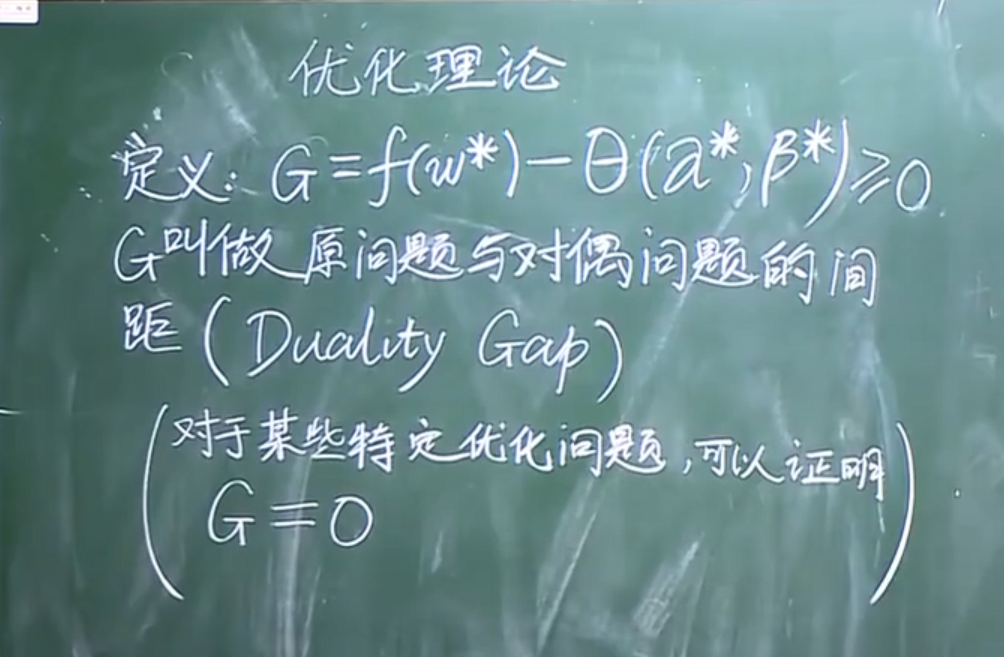
这里可以去看《Convex optimization》前150页内容，学习推导过程。

结论可推出：

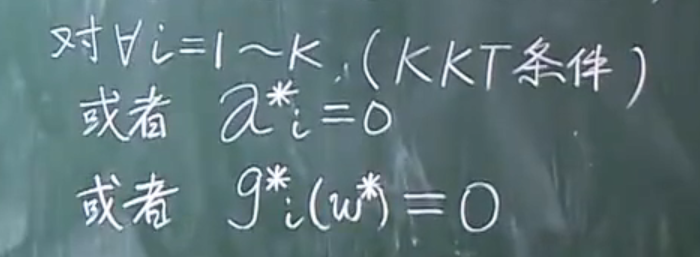
支持向量机原问题转化为对偶问题==(重点复习)==

凸函数的定义。w可能是高维向量，这个代数表达在高维依然适用。

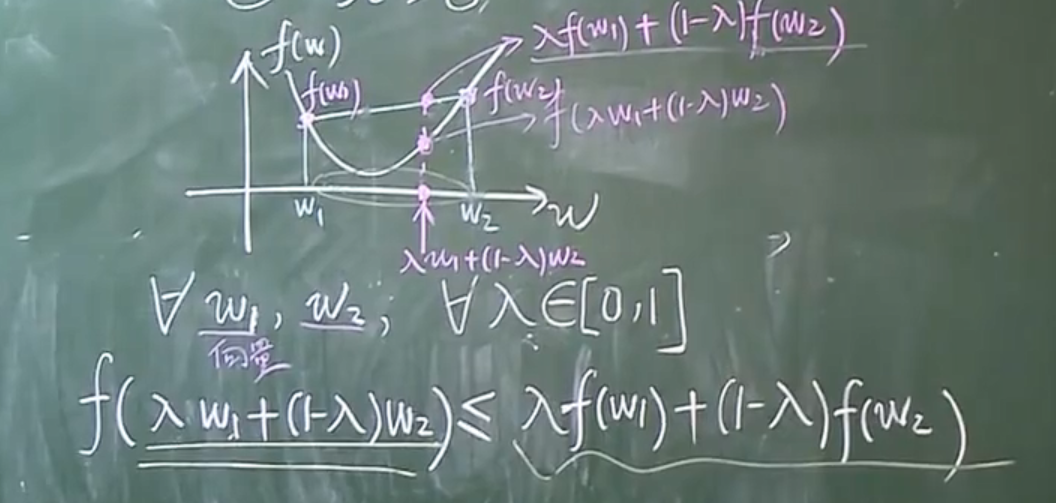
原问题证明建议重看p12-23:37

支持向量机的应用——兵王问题

n折交叉验证

对于每一组超参数，进行n折交叉验证求损失，最终选取的是损失最小的那一组超参数。

测试结果中的支持向量

当支持向量占比非常高，甚至是几乎等于训练样本。则表明这次训练失败，或者数据集本身没有规律，或者SVM 没法找到他的规律。

评判模型好坏

混淆矩阵

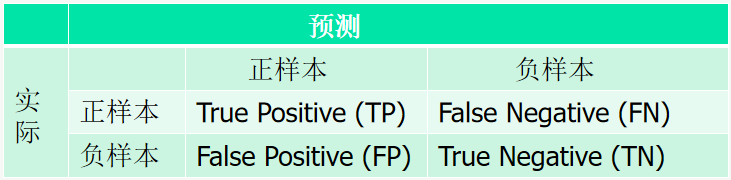
TP: 将正样本识别为正样本的数量（或概率）

FN: 将正样本识别为负样本的数量（或概率）

FP: 将负样本识别为正样本的数量（或概率）

TN: 将负样本识别为负样本的数量（或概率）

FN减少 <=> TP增加 <=> FP增加 <=> TN减少

mAP: mean Average Precision, 即各类别AP的平均值

AP: PR曲线下面积，后文会详细讲解

PR曲线: Precision-Recall曲线

Precision: TP / (TP + FP)

Recall: TP / (TP + FN)

TP: IoU>0.5的检测框数量（同一Ground Truth只计算一次）

FP: IoU<=0.5的检测框，或者是检测到同一个GT的多余检测框的数量

FN: 没有检测到的GT的数量

ROC曲线(Receiver Operating Character)

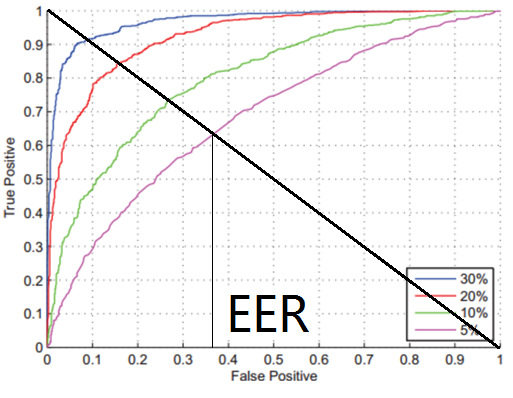
四条线表示四个不同的系统

等错误率 (Equal Error Rate, EER)是两类错误FP和FN相等时候的错误率，这时错误率越小，表示系统性能约好。

AUC(Area Under Curve)曲线右下角的一块面积，面积的大小也能体现模型的好坏。

判别模型的好坏要看具体的应用，并不是准确率越高，模型高就越好

兵王问题的Python实现==(补充)==

处理多分类问题

1. 改造优化的目标函数和限制条件，使之能处理多类
   论文 SVM-Multiclass Multi-class Support Vector Machine
2. 一类 VS 其他类
3. 一类 VS 另一类

其中，①方法通常不是很好，因为SVM是针对二分类问题开发的。

在n类问题分类中，②方法主要构造n个SVM，③方法要构造 n * (n-1) / 2 个SVM。

通常来说，③方法分类噢效果更好，但是也更复杂。