PyTorch深度学习实践Part6——逻辑斯蒂回归

分类问题

逻辑斯蒂回归是处理分类问题，而不是回归任务。

处理分类问题，不能使用回归的思想，即使输出可以为0或1。原因在于：若有一个0-9，10个手写数字的分类问题，在回归模型中，1和0距离很近，0和9离得很远，但是在分类模型中，7和9的相似度就比8与7或9的相似度要高。

分类问题本质上输出的是概率，例如P(0)、P(1)…。

二分类问题

通过考试的概率是多少

多分类问题

0-9手写数字检测分类

torchvision工具包

指定目录，训练/测试，是否需要下载

MNIST、CIFAR10…

1
2
3
import torchvision
train_set = torchvision.datasets.MNIST(root='../dataset/mnist', train=True, download=True)
test_set = torchvision.datasets.MNIST(root='../dataset/mnist', train=False, download=True)

饱和函数

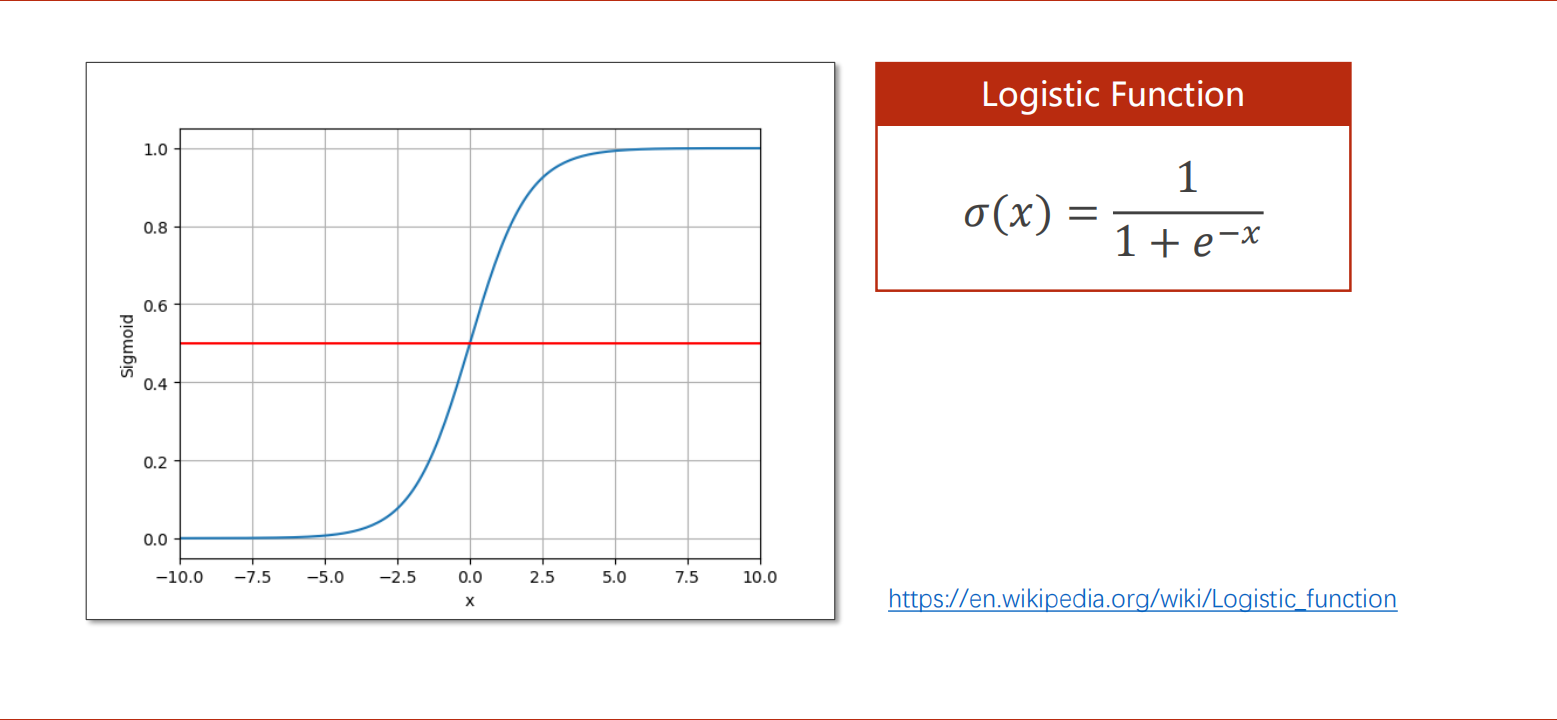
逻辑斯蒂函数

image-20210117161720715

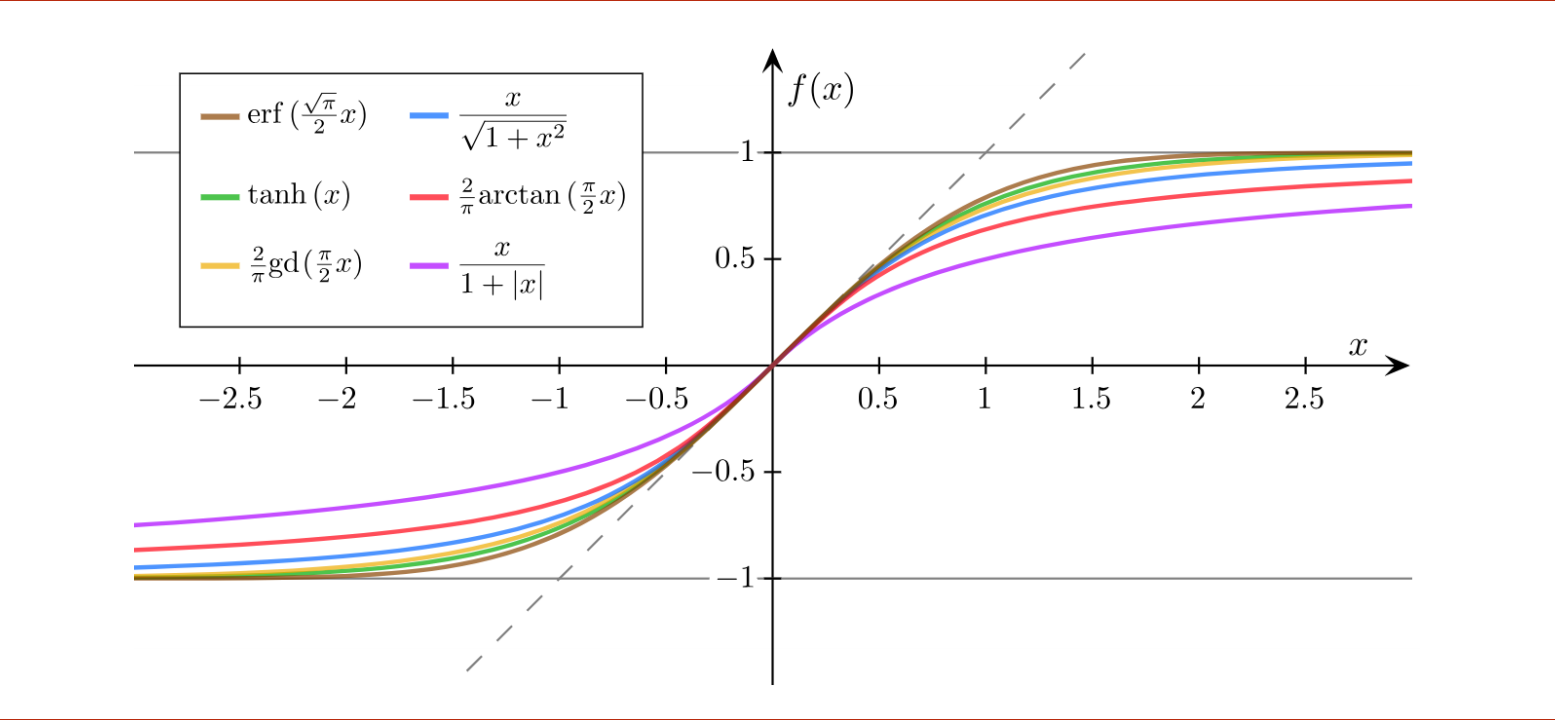
其他Sigmoid functions

image-20210117161834404

逻辑斯蒂回归

  1. Logistic Regression类似于正态分布。

  2. Logistic Regression是Sigmoid functions中最著名的，所以有些地方用Sigmoid指代Logistic。

  3. 逻辑斯蒂回归和线性模型的明显区别是在线性模型的后面，添加了激活函数(非线性变换)，将y_hat代入逻辑斯蒂公式中的x。

  4. 交叉熵损失函数的推导过程与直观理解

  5. y_hat是预测的值[0,1]之间的概率，y是真实值，预测与标签越接近，BCE损失越小。

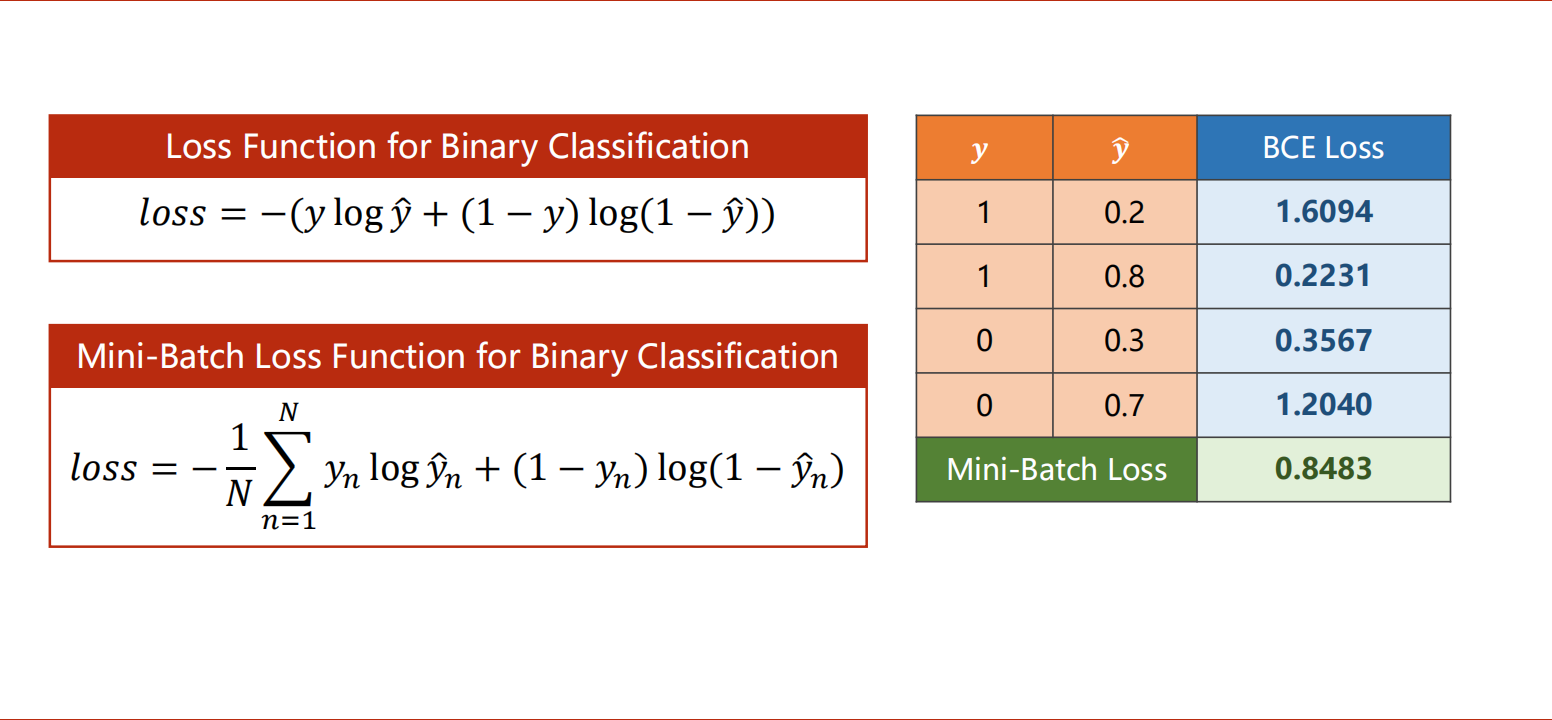
image-20210117164616620

要计算的是分布的差异，而不是数值上的距离

代码实现

  1. torch.sigmoid()、torch.nn.Sigmoid()和torch.nn.functional.sigmoid()三者之间的区别
  2. BCELoss(Binary CrossEntropyLoss)是CrossEntropyLoss的一个特例，只用于二分类问题，而CrossEntropyLoss可以用于二分类，也可以用于多分类。
  3. BCE和CE交叉熵损失函数的区别
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
import torch
import matplotlib.pyplot as plt

# ---------------------------Prepare dataset----------------------------#
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])  # 二分类


# ---------------------------Design model using Class----------------------------#

class LogisticRegressionModel(torch.nn.Module):
    def __init__(self):
        super(LogisticRegressionModel, self).__init__()
        self.linear = torch.nn.Linear(1, 1)

    # nn.functional.sigmoid is deprecated
    def forward(self, x):
        return torch.sigmoid(self.linear(x))  # 激活函数sigmoid不需要参数训练，直接调用


model = LogisticRegressionModel()
# --------------------------Construct loss and optimizer-----------------------------#
criterion = torch.nn.BCELoss(reduction='sum')  # 交叉熵，size_average=False已经被弃用
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
# --------------------------Training cycle-----------------------------#
loss_list = []

for epoch in range(1000):
    y_pred = model(x_data)  # 正向传播
    loss = criterion(y_pred, y_data)  # 计算损失
    print(epoch, loss.item())
    loss_list.append(loss.item())  # 保存loss

    optimizer.zero_grad()  # 将梯度归零
    loss.backward()  # 反向传播
    optimizer.step()  # 进行更新

print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())

x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.item())

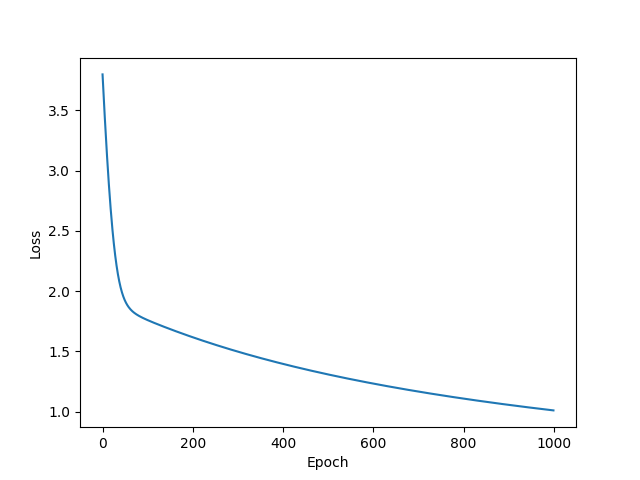
plt.plot(range(1000), loss_list)
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.show()
# y_pred =  0.8808996081352234

image-20210117172329760